Do all solids sublimate at low enough temperature and pressure?

Question

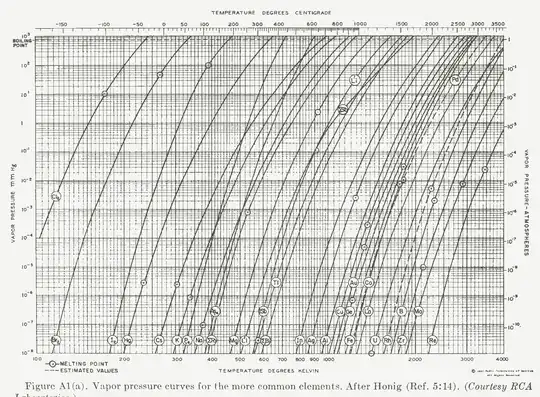
When we look at the phase diagram of a material, at low enough temperature and pressure, it tends to sublimate:

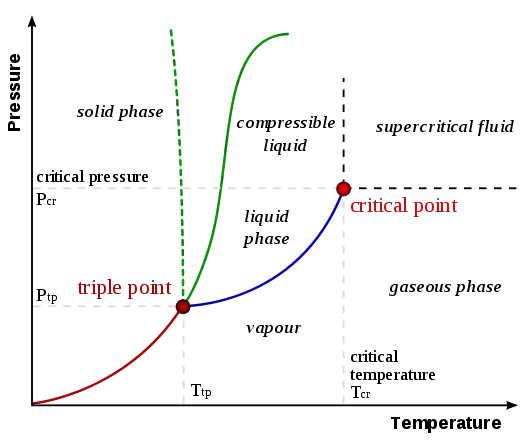So can it be true that no matter how strong a solid is, if at a low enough temperature, I maintain pressure below a certain level, it is bound to sublimate.

But is this true for all solids, no matter how strong the bonding is and no matter how much energy has been lowered by formation of solid?? on Wikipedia page, even common metals seem to sublimate (https://en.wikipedia.org/wiki/Materials_for_use_in_vacuum)

Suppose I consider a simple chain with nearest neighbour hopping, the electrons occupy the valence band with energy as $-2t_0(1-\cos(ka))$ where $t_0$ is nearest neighbour hopping, this total energy is negative hence shouldn't the solid be always energetically favourable than separate atoms roaming in space (if phonons are not energetic enough to break the chains)??

I am thinking taking into account the thermodynamics of photons and phonons is also important but I am not able to think of their role in this

Answer 1

Yes, all condensed matter is expected to spontaneously sublimate/evaporate at any pressure and temperature. (Put another way, all materials have a nonzero vapor pressure.)

The standard argument is that the first molecule that detaches and flies off into the void increases the entropy of the universe by a tremendous amount due to the new positional opportunities. In Gibbs free energy terms, this is more than enough to offset any enthalpy penalty arising from bond breaking during detachment. Minimization of the Gibbs free energy can in turn be traced back to the Second Law (derivation sketch).

The equilibrium vapor pressure increases somewhat with increasing total pressure because the strain energy stored in the condensed matter increases the relative stability of the gas phase. This dependence is typically small and often ignored.

More importantly, the vapor pressure is a strong—exponential—function of the temperature and decreases to essentially zero (but not exactly zero) as the temperature decreases toward 0 K:

(Larger version here.)