The confusion here is about a direction of a wave versus its polarization. Even sound waves can be longitudinal and transversal, depending on whether the particles in a wave oscillate along the direction of the wave propagation or perpendicular to it. Such transversal waves cannot exist in liquids and gases, but necessarily present in solids. A string of a musical instrument is also a good example of sound wave that is not longitudinal.
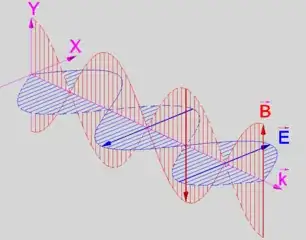
Electromagnetic wave (in vacuum) has its magnetic and electric fields oscillating in directions perpendicular to the wave vector (i.e., the direction of the wave), hence it is a transversal wave. This is not always the case for electromagnetic waves in media, where longitudinal component may emerge.
The Wikipedia article on Polarization formulates this as:
Polarization (also polarisation) is a property applying to transverse waves that specifies the geometrical orientation of the oscillations.1[3][4][5] In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave.[4] A simple example of a polarized transverse wave is vibrations traveling along a taut string (see image); for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves,[6] and transverse sound waves (shear waves) in solids.
An electromagnetic wave such as light consists of a coupled oscillating electric field and magnetic field which are always perpendicular to each other; by convention, the "polarization" of electromagnetic waves refers to the direction of the electric field. In linear polarization, the fields oscillate in a single direction. In circular or elliptical polarization, the fields rotate at a constant rate in a plane as the wave travels. The rotation can have two possible directions; if the fields rotate in a right hand sense with respect to the direction of wave travel, it is called right circular polarization, while if the fields rotate in a left hand sense, it is called left circular polarization.
Comment
Let us consider a wave of an arbitrary nature for a vector quantity:
$$
\mathbf{A}(\mathbf{x},t)=\mathbf{A}\cos(\mathbf{k}\cdot\mathbf{x}-\omega t).
$$
The wave front is the surface where the quantity is the same, i.e., where the value of the argument of the cosine function is the same:
$$
\mathbf{k}\cdot\mathbf{x}-\omega t=c
$$
It is easy to see that this surface propagates with velocity
$$
\mathbf{v}_{ph}=\frac{\mathbf{k}\omega}{k^2}, |\mathbf{v}_{ph}|=\frac{\omega}{k}.
$$
(this is a so-called phase velocity, not to be confused with the group velocity, see here)
The direction of this velocity is the same as that of $\mathbf{k}$, but completely unrelated to that of $\mathbf{A}$, which depends on the nature of the wave. By analyzing the derivation of waves (or wave equations) in different media, one can see that in liquids or gases, where the layers of matter are moved by excess or lowering of pressure, the direction of the particle movement can be only in the same direction as $\mathbf{k}$. However in solids, the existence of a shear stress leads to the possibility of transversal waves. Same is true for EM field, as can be seen from the Maxwell equations.
To restate the point differently: the particles (or the fields in the wave) are not moving along with the wave - they are oscillating near the same equilibrium position. The propagation of a wave has to do with the propagation of the phase surface (the "wave front"), not with the actual direction of motion of the matter or fields.