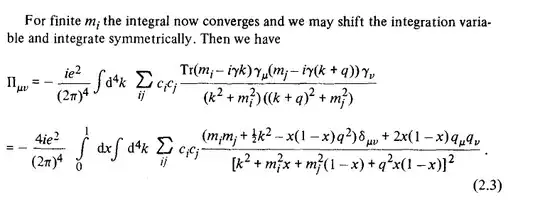I always wanted to understand what re-normalization in particle physics really means. Having a background in statistical physics I do understand it in there but as far as I know re-normalization in particle physics is different; it has to do with removing infinite contributions to series expansion terms of the scattering matrix amplitudes. In other words certain Feynman diagrams, when computed naively, are divergent and one performs some tricks to obtain finite quantities.
Now, in order to understand what those tricks are I decided to study the paper by Gerard 't Hooft 1, a paper that supposedly earned him a Nobel prize in physics. In chapter 2 in page 175 the author computes the so called photon self-energy, meaning a probability amplitude for a photon to create a virtual positron-electron pair that is short lived and annihilates after a while. The original integral is infinite because the integrand grows quadratically with the momentum $k$-vector for large values of $k$.
The author replaces the electron propagator by a linear combination of similar propagators with certain constraints being imposed on the coefficients. As far as I can see those constraints have an effect that they remove those quadratic contributions to the integral at infinity and as a result it is possible to make that integral finite. But now I got completely stuck on top of the next page meaning in equation (2.3) which reads as follows:
In the left hand side we have an integral over the space time and on the right hand side, in addition to that integral , we have some new scalar quantity $x\in [0,1] $. Now, my question would be twofold, firstly can anyone explain to me how this equality has been obtained? Is this an exact equality or some sort of approximation? What does the author mean by "integrating symmetrically"?
1 G.'t HOOFT, Renormalization of massless Yang-Mills theories, Nuclear Physics B33 (1971) 173-199. https://webspace.science.uu.nl/~hooft101/gthpub/massless.pdf