What are the properties of the virtual photons that transmit forces in electrostatics?

Question

I gather that in quantum mechanics the interaction between two charged particles is explained by the exchange of virtual photons. These virtual photons cannot be measured but are implied from the measured change in momentum of the particles before and after the interaction. For a single interaction of a pair of fundamental particles (e.g. electrons), it would seem that the exchange of a single pair of photons with the required momentum would do the job. This implies a pair of virtual photons with a well-defined frequency or wavelength.

But what happens for electrostatics? The forces are presumably attributed to the flow of momentum associated with a continuing exchange of virtual photons. It seems like I'm free to define the rate at which virtual photons are exchanged. This then would define the momentum per photon, since the product of the two quantities must yield the required force. The fact that the momentum/energy/frequency/wavelength of these virtual photons is not well defined doesn't seem like a very satisfactory conclusion, but is this the correct understanding? Or is there something else in the specific configuration that would further confine the solution and help define the frequency of the virtual photons?

I see a similar question asked and answered here. I find the answer difficult to understand, but maybe this question is more focussed (or maybe it just painfully exposes my ignorance of the topic)

Answer 1

The term "virtual" is used for all particles contributing to an interaction that can be modeled with Feynman diagrams, when they are internal lines in the diagrams. For photons particularly

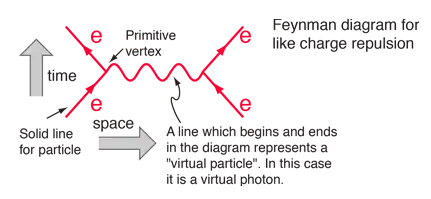
The line has the name of the corresponding particle because in addition to representing the four momentum $(E,p_x,p_y,p_z)$, transferred in the interaction, it carries the conservation of quantum numbers between vertices. The line has the attributes of the named particle, except the mass is off shell. In the above diagram, the photon has a non zero mass in the integral represented by the diagram, and the four momentum it carries varies between the limits of integration. That is why it is called virtual. It is only incoming and outgoing lines that can be measured and tested against the calculations. The fact that the calculations are successful in predicting crossections has validated the Feynman diagram approach.

You ask:

But what happens for electrostatics? The forces are presumably attributed to the flow of momentum associated with a continuing exchange of virtual photons. It seems like I'm free to define the rate at which virtual photons are exchanged.

For electrostatic forces the mathematical way is given in the answers to this question

The classical Coulomb potential can be recovered in the non-relativistic limit of the tree-level Feynman diagram between two charged particles.

It still depends on integrals over the variables of the exchanged photon:

An integral means that there is a continuous change in the virtual photon four vector, $(E,p_x,p_y,p_z)$ and depends on the limits of integration. No, you are not free to define anything. It is all constrained by the mathematics of computing Feynman diagrams, where virtual particles have a definition.

You ask:

The fact that the momentum/energy/frequency/wavelength of these virtual photons is not well defined doesn't seem like a very satisfactory conclusion, but is this the correct understanding?

The four vector of the virtual photon is incrementally defined within the limits of integration. For example, in the integral

$$ \int_0^4x\ \mathrm dx $$

the value of x changes continually between 0 and 4. In the same way the four vector of the exchanged particle within the Feynman integral limits varies continuously.

Or is there something else in the specific configuration that would further confine the solution and help define the frequency of the virtual photons?

The frequency of the virtual photon depends on the $E$ of the four vector and varies continuously in the integration.

Edit : a simpler answer for the non physicality of the virtual photon in the diagram above is that from conservation of energy and momentum, and the fact that the two electrons have mass , the summed four vector has an invariant mass . This means the virtual photon carrying the four vector has a mass, which means it is not a real photon, as photons have mass zero.

Answer 2

There are virtual photons but they are not arbitrarily defined.

A Feynman diagram such as

shows the scattering of two electrons with momentum $p$ and $k$ into two electrons with momentum $p'$ and $k'$. The important part of this diagram is, at each vertex the momentum is conserved, so the virtual photon here must have momentum $p-p'$. The reason Feynman diagram describe the interaction of electrons with definite momentum instead of position is pragmatic, because this where the interaction is simplist to calculate.

This is interaction between electrons with a definite momentum. As we know in quantum mechanics, position and momentum cannot be determined simultaneously. So if we are trying to describe some static charged object and some other static charged object, we have to break down quantum state as a superposition of all these definite-momentum electrons, calculate the interaction for each pair of momentum states, and then sum up the over all effect. This is probably pretty complicated business, but it can be done theoretically, and we'd be able to calculate the interaction precisely. So there has to be a specific distribution (in momentum space) of virtual photons, which contribute to the interaction between two static charged objects.