Molecular origin of solid-liquid and solid-vapour surface tension

Question

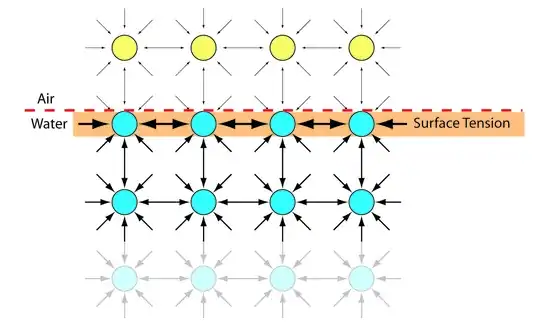
I understand that surface tension arises at the liquid-vapour interface due to the asymmetric nature of long-range attractive forces and the short-range repulsive forces acting on the interface where there exists a gradient of density as we go from the liquid phase to the vapour. As explained by Michael Berry^[1], the short-range repulsive interaction, which is proportional to the density, decreases faster compared to the long-range attractive force, when going from the bulk to the vapour.

But I don't understand how the surface tension arises in the case of a solid-liquid interface. Solid particles are tightly bound to each other and I don't think that there exists a smooth density gradient at the solid-liquid interface. So, how does a surface tension force which is parallel to the interface arise in this case?

Same question for the solid-vapour interface. I'm not even sure if there can exist a surface tension force parallel to the solid-vapour interface; apparently the 'surface tension' force is just a reaction force from the surface molecules as a response to deformation.^[4]

I would prefer an explanation in terms of molecular forces rather than in terms of thermodynamic arguments. Thermodynamic arguments can prove that if the system adopts some configuration, then it is stable there. But this does not shed any light on the actual mechanism of how the system adopts the configuration, in mechanical terms of forces.

I've read the following references but have failed to understand the solid-liquid and solid-vapour cases.

1. Berry, Michael V. ‘The Molecular Mechanism of Surface Tension’. Physics Education, vol. 6, Mar. 1971, pp. 79–84. NASA ADS, doi: 10.1088/0031-9120/6/2/001. PDF (available from author's website): https://michaelberryphysics.files.wordpress.com/2013/07/berry018.pdf.
2. Why is surface tension parallel to the interface? https://physics.stackexchange.com/q/150853.
3. Marchand, Antonin, et al. ‘Why Is Surface Tension a Force Parallel to the Interface?’. American Journal of Physics, vol. 79, no. 10, Sept. 2011, pp. 999–1008. aapt.scitation.org (Atypon), doi: 10.1119/1.3619866. arXiv: https://arxiv.org/abs/1211.3854.
4. Makkonen, Lasse ‘Misinterpretation of the Shuttleworth equation’ Scripta Materialia, vol. 66, no. 9, 2012, pp. 627-629, doi: 10.1016/j.scriptamat.2012.01.055. PDF: https://cris.vtt.fi/en/publications/misinterpretation-of-the-shuttleworth-equation.

---

Edit:

My understanding of the solid-liquid surface tension is as follows. Please correct me if it is incorrect.

Liquid particles near the solid surface are attracted towards the solid surface and thus there is a slight increase in liquid density near the interface. This increased density causes increased pressure and this pressure gives rise to a tangential force in the liquid at the solid-liquid interface. But this force is not equal to the solid-liquid surface tension. This is what is written in the third reference. I don't understand why this is the case.

---

Second edit:

A new pre-print claims, if I understand correctly, that the downward acting force in Young's diagram, opposite to $\gamma_\text{lv}\sin\theta$, is due to vaccum polarization. $\gamma_\text{lv}$ is the liquid-vapor surface tension, and $\theta$ is the contact angle. References:

1. Rouslan Krechetnikov and Andrei Zelnikov ‘Vacuum polarization at the tip of a water drop’. arXiv: https://arxiv.org/abs/2408.05833v1.
2. Rouslan Krechetnikov and Andrei Zelnikov ‘Nonretarded limit of the Lifshitz theory for a wedge’ Physical Review A, vol. 105, issue 2, Feb 2022, American Physical Society. doi: 10.1103/PhysRevA.105.022802. arXiv: https://arxiv.org/abs/2103.16715.
3. Rouslan Krechetnikov and Andrei Zelnikov ‘Scarf for Lifshitz’ European Physical Journal Plus, vol. 136, issue 7, July 2021. Springer Science and Business Media LLC. doi: 10.1140/epjp/s13360-021-01714-3. arxiv: https://arxiv.org/abs/2103.16713.

Answer 1

I like to think in terms of energy principles.

Think of a solid, and pick an atom deep in the solid. It will (presumably) have chemical bonds in all directions. It is important to realize that, it needs energy to break one of these bonds: the atoms prefer to have these bonds, as opposed not to.

Now pick an atom at the surface of a solid. Imagine an horizontal interface. Below there's the solid. Above there's something else - liquid or gas. Below the interface, the atom has its bonds, as it should, but above the interface, there are no ways to make these bonds, because, there's no longer the solid up there, but something else - its equivalent of thinking the bonds have been broken. In other words, this atom would rather be down, deep in the solid, than on the surface of the solid, where it can only bond to half the atoms.

The moral of the story is: to create a surface is an energetic costly event (you need to break bonds to do so). The cost of energy payed to create a surface of area $A$, is the very definition of surface tension: $dE = \gamma dA$.

In other words, in terms of molecules: $$ \gamma = \frac{W}{A} = \frac{\text{energy payed by bonds not happening at the surface}}{\text{the area of the surface that was created}} $$

For example, in a liquid-air interface, because creating a surface of area $A$ has an energy penalty of $\gamma A$, the liquid will prefer to occupy the most volume, in the minimum surface area possible - a sphere. This happens in zero-G environment, or when gravitational potential energy (which scales with volume), is too weak to overpower surface tension energy (which scales with area) -- very small portions of fluid, say, droplets of water.

This explanation works for any type of interface: Liquid-air interface, liquid-liquid interface, solid-air interfaces, solid-liquid interfaces, solid-solid interfaces, .....

Answer 2

Surface tension is basically just molecular attraction. Or actually the lack of it. Solids and Liquids, condensed matter generally, exists solely due to the fact that temperature based particle velocity is too low, that the molecules can exit this molecular attraction. $$v_{rms}=\sqrt{\frac{3k_BT}{m}}$$

At the surface, the molecules have less attractive counterparts, as when they are fully surrounded by them inside the fluid/solid, and thus their attraction is divided to the fewer molecules, and is thus stronger. It is fully possible, that there is no (or minimal) surface tension or that there exists almost full surface tension between liquid-liquid or liquid-solid. Lack of surface tension also means solvation over time, as the molecules are equally attracting each other; it is possible to build a drink where water is on bottom and ethanol on top, and they even remain this way for some time due to the density difference, but given enough time they will fully dissolve and finally create a homogen mixture. An opposite example of an Liquid-liquid interface would be mercury and water.

The solids, which lacks the attraction to water are called Hydrophobe, and solids which attract are called Hydrophile. The amount of this attraction or the absence of it, is commonly measured by the contact angle.

This is the reason why soap destroys the surface tension; It simply disturbs the molecular attraction of water; soap molecules do not stick together -> Absence of attraction -> No surface tension.

Answer 3

Gases can be modeled as weakly interacting molecules, but solids and liquids have strong atractive forces. Besides that, molecules have kinetic energy in all of them.

Let's analyse the collision of a liquid vibrating molecule to the solid wall. If the effect of the wall was to bounce back it like a mirror surface, that is: the angle of incidence being equal to the angle of reflection, the linear momentum in the directions parallel to the wall would not be affected (by the wall). As $$\mathbf F = \frac{\mathbf {dp}}{dt}$$ and pressure is force by area, the consequence would be no pressure parallel to the wall induced by it.

But the solid also have vibration molecules, so there is no reason to expect such a mirror effect. It is more realistic to compare with light being scattered by a non-mirror wall. In that case, each collision also changes the momentum in directions parallel to the surface. That leads to surface forces and surface pressure.

The same reasoning can be made for the interface liquid-vapour, because the molecules of gas also scatter the vibrating liquid molecules.

Answer 4

First, the surfaces of many solids are actually not crystalline, but amorphous. This goes under the name of "quasi-liquid layers" or "premelting". So the situation for a solid is not entirely different from that of a liquid. However, I believe a surface tension can be defined for a solid even without a quasi-liquid layer.

The way I think about it is it to view surface tension as energy per area. After all, the unit [N/m] is also [J/m²]. The surface energy (= tension) comes about as the difference in energy for being on the surface rather than in the interior, which is due to the asymmetry of the molecular forces. The surface energy of a solid can be measured by the adhesive force between two surfaces made of the same material. For example, two pieces of water ice adhere to each other and it takes the same force to separate them again. Same for two plane pieces of mica.

The surface tension is also related to the vapor pressure and the latent heat, which are as well-defined for a solid as they are for a liquid. The surface tension of the solid-vapor interface is the sum of those for the solid-liquid and liquid-vapor interfaces, just as the latent heat of sublimation is the sum of the latent heats for melting and evaporation.

Hope that helped.