What determines whether two quantum particles will "interact?"

Question

The concept of quantum particles interacting is confusing to me. By "interact" I mean that thing particles do where they become entangled and exchange information and wavefunction collapse occurs. It's why quantum particles often appear to behave classically. But quantum particles don't have definite borders or definite locations, so they can't touch, and there's no point at which their wavefunctions will start overlapping, since the wavefunctions don't have borders past which the probability density is zero. Is there some sort of threshold, or is interaction actually a greyscale thing, where the closer they are, the more "intensely" they'll interact? Do the four fundamental interactions have anything to do with it?

Answer 1

If the two-particle Hamiltonian cannot be written as the sum of one-particle Hamiltonians, then the particles always were and always will be interacting. If the Hamiltonian is \begin{equation} H_0(x_1, p_1) + H_0(x_2, p_2) + V(x_1, x_2), \end{equation} a sensible initial state (for bosons) to prepare is \begin{equation} \Psi(x_1, x_2, 0) = \frac{1}{\sqrt{2}} \left [ \psi_a(x_1) \psi_b(x_2) + \psi_a(x_2) \psi_b(x_1) \right ] \end{equation} where the $\psi_i$ are eigenstates of $H_0$. Because of the interaction potential, $\Psi$ is not an eigenstate of the total Hamiltonian. So the moment you let it evolve,the two particles will become entangled. Therefore there is never an open neighbourhood of time for which you could've talked about their separate wavefunctions to begin with.

Indeed, it might be the case that it takes awhile before this interaction is intense enough for us to detect it. This will happen if $\psi_a(x) = \delta(x - x_a)$ where $x_a$ and $x_b$ are much farther apart than the length scale set by $V$.

Answer 2

To get a sort of intuition: You can think of "forces" in quantum mechanics as acting on the wavefunctions (the probability amplitudes) of the particle. So for instance, a "force" might cause a wavefunction to become broader. A quantum mach-zhender interferometer, for example, causes these waves to interfere with themselves, which ends up changing which way the particle goes.

Likewise, a force that interacts with 2 particles, now there are two separate wavefunctions to consider, and this force will cause the components of each wavefunction to change when there is an overlap between the two particle's wavefunctions.

[Digression: I think in principle nothing stops you from defining a nonlocal force in which a wavefunction at location. A interacts with a wavefunction at location B - but it's generally considered that such "nonlocal" forces don't exist. (A lot of times, we assume from first principles that such nonlocal forces cannot exist.)]

Anyway, if you have a local force, that force will cause an interaction between two states for the component of the wavefunction that is overlapping. (This interaction could create something like entanglement, as discussed in this question. In the end, the components of the wavefunctions that overlap end up having an interaction and might change, while the parts of the wavefunction that do not interact will stay the same.

Answer 3

What determines whether two quantum particles will “interact?”

The coupling constants and the quantum numbers that the particle carries will determine how probable an interaction is.

By "interact" I mean that thing particles do where they become entangled and exchange information and wavefunction collapse occurs.

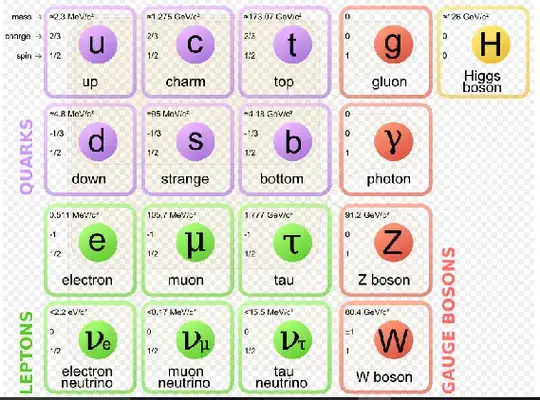
Look at the table of elementary particles for simplicity:

They carry lepton number or baryon number or strangeness or color, all these determine when setting up an experiment of scattering one particle against another, how probable it will be that they will interact. This is done using Feynman diagrams that allow to write down the integrals on the probability of interaction, the cross section.

It's why quantum particles often appear to behave classically. But quantum particles don't have definite borders or definite locations,

elementary particles are described, when non interacting, by the solution of the appropriate one of the wave equations that carry the correct quantum numbers for those particles, without any potential.This is plane waves and cannot be used to describe a free particle as one has to have finite probability for the location of the particle. One has to use the wave packet solutions if one wants to model a non interacting particle.

so they can't touch, and there's no point at which their wavefunctions will start overlapping, since the wavefunctions don't have borders past which the probability density is zero.

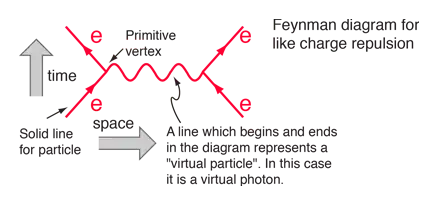
If two free particles approach each other one uses the formalism of quantum field theory and Feynman diagrams to describe the interaction ( not the cumbersome wave packets).

With Feynman diagrams, each of the four forces has a gauge boson, which may be exchanged between the particles, example:

This is how one can calculate the repulsion between two electrons in QED. The force can be understood as an exchange of momentum dp/dt before and after the interaction and the calculation gives how probable it is to interact. This means that the experiments have to happen with the exact same boundary conditions, and one has to accumulate data in order to see whether the calculation describes the data (it does)

Do the four fundamental interactions have anything to do with it?

Yes, the couplings give the strength of the interaction, and the first order diagrams exchange the gauge boson.

In general virtual particles in the Feynman diagrams carry the dp/dt, the force of the interaction.