0

Suppose I have a tennis ball moving with $v_1$ (blue arrow in first image below) impacting a moving tennis racket with velocity $v_r$ (black arrow in first image below) 1

In order to calculate the velocity of the ball after the bounce, it is helpful to imagine that the racket is static. To do this, I take the relative velocity of the ball with respect to the racket as follows: $$v_{\text{rel}} = v_1 - v_r$$

This gives me the red arrow in the 2nd image below: 2

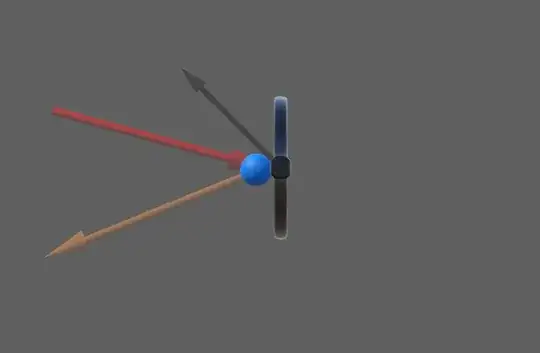
Now if the racket is completely still, with an incoming velocity of $v_{\text{rel}}$ (red arrow), it will bounce with a result similar to the orange arrow.

My question is, in order to get the true velocity of the ball after the collision $v_2$, do I need to add on the racket's initial velocity to the result calculated in the static reference frame (i.e. add the black arrow to the orange arrow)? Or is this effect already accounted for by taking the relative velocity?

If the answer is no, you don't need to add the rackets initial velocity, that implies that the faster the racket is moving upward, the more the ball will move downward after collision - which seems somewhat counterintuitive.

Vincent Thacker
  • 15,416
Adrian Taylor
  • 103

1 Answers1

2

My question is, in order to get the true velocity of the ball after the collision $v_2$, do I need to add on the racket's initial velocity to the result calculated in the static reference frame (i.e. add the black arrow to the orange arrow)?

Yes, you need to, because you are first going into the reference frame of the racket by subtracting $v_r$ from every object. In this frame, the ball comes in with $v_{\text{rel}}$ and bounces off with $v_{\text{rel}}'$. You then need to transform $v_{\text{rel}}'$ back to the lab frame, which means adding $v_r$ back to every object.

In one dimension, this is straightforward as described in this post. The velocity simply reverses direction and increases by twice the velocity of the racket.

However, in three dimensions, this is not always the case; you need to consider vector addition and subtraction.

Vincent Thacker
  • 15,416