0

If we have a potential of the form $V(x,y)=k_{x}x^{2}+k_{y}y^{2}$ then that potential looks like this: 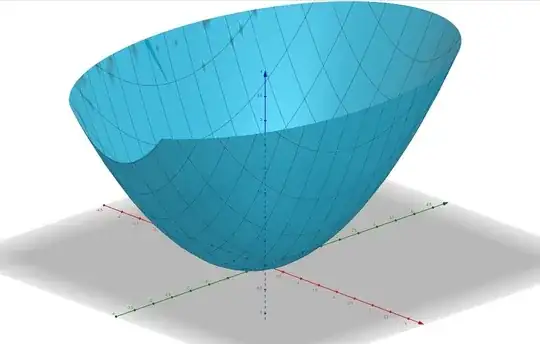A 3d plot of V against x,y As you can see, this potential is clearly round. When dealing with simple harmonic oscillators (like a pendulum free to swing in 2 directions for small swings) then the behaviour we see is clearly... rounded. What I think I mean by this is if $k_x = k_y$ that the SHO in question needs more energy to reach somewhere based only on the euclidean distance from the equilibrium point and if they are different it's only a question of scaling the dimensions first.

Why is it then, that when I render out the 2D QHO what I get is decidedly rectangular.

Rendering of the QHO in motion

This rendering uses hue for argument and brightness for magnitude.

Since it is possible I am using the wrong approach I will say that the eigenstates I am using are $\Psi_{n_x,n_y}(x,y,t)=X(x)\cdot Y(y)\cdot \phi(t)$ where $X$ and $Y$ are only different in their variables and values of k but are of the form $$\psi_{n}(\sqrt{\alpha}x) = \left(\frac{\alpha}{\pi}\right)^{1/4} \cdot \frac{1}{\sqrt{2^{n}n!}}\cdot H_{n}(\sqrt{\alpha}x) e^{-\frac{\alpha x^{2}}{2}}$$ And $\alpha = \sqrt{\frac{mk}{\hbar^{2}}}$ and $\phi(t)=e^{-itE/\hbar}$

From what I've read it seems like this should behave as though it had the potential described but for any values of k that I tried and for any superposition of states I could think of it still ends up looking rectangular.

Is this what I should expect? If so then why is the quantum case so different? Is my code wrong? If so where in my reasoning is the misstep?

Disgusting
  • 826

2 Answers2

2

When looking for solutions to the Schrodinger equation that exhibit a particular symmetry, it's best to use coordinates which mimic this symmetry. You used Cartesian coordinates, and so the basic solutions you find will inevitably have rectangular symmetry.

As an example for how this works for the 2d quantum harmonic oscillator when $k_x=k_y$, look at @CosmasZachos 's answer to 2D isotropic quantum harmonic oscillator: polar coordinates.

fewfew4
  • 3,574
0

My bet would be that it's because you're plotting magnitude instead of magnitude squared (probability amplitude), combined with your specific initial conditions of the wave function. Square rooting probability amplitude could amount to something like using a different kind of "norm". Although rectangularity more likely points to something like the maximum norm. It is difficult to say if and what you are doing wrong without seeing your code.

As an illustration for what I said about the initial conditions, consider separating variables $x$ and $y$ which gives you a solution that is a product $$\psi(x,y,t)=\psi_1(x,t)\cdot \psi_2(y,t)$$ So if you choose for both factors a moving wave packet solution, forming the product is a little like moving from left to right and back a paper with a vertical bar cut out, and crossing this with a paper with a horizontal bar cut out, and moving it up-down and back. The result would always look "rectangular", I guess. So it is an artifact of choosing your specific solution, which is what fewfew4 has emphasized in his answer, as far as I have understood.

oliver
  • 7,624