1

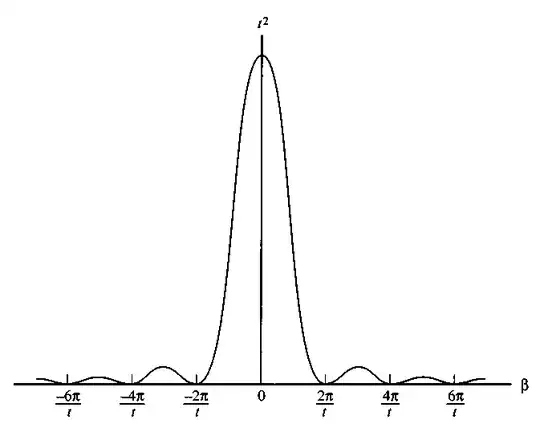
For a constant perturbation of the form $$\hat{H'}(t)=\hat{V}\theta(t)$$ to a time-independent Hamiltonian $\hat{H}_0$, the transition probability at time $t$ from an eigenstate $|i\rangle$ of $\hat{H}_0$ with energy $E_i$ at $t=0$ to a final state $|f\rangle$ ($\neq |i\rangle$) is given by $$P_{i\to f}(t;\omega_{fi})=|V_{fi}|^2\left[\frac{\sin(\omega_{fi}t/2)}{\omega_{fi}/2}\right]^2$$ where $\omega_{fi}=(E_f-E_i)/\hbar$. At a fixed $t$, the transition probability $P_{i\to f}(t;\omega_{fi})$ peaks at $\omega_{fi}=0$ i.e., for $E_f=E_i$. Why does a constant perturbation favour the transition at $\omega_{fi}=0$? Is it because the constant perturbation has only $\omega=0$ frequency component? But then why don't we see a delta function peak at $\omega=0$?

enter image description here

Solidification
  • 12,736

2 Answers2

2

Your perturbation is by no means constant as it has a step function, which has all frequencies in its Fourier transformation. For such violent step-function perturbations you should use the "sudden" approximation in which the transition amplitude is simply the overlap between the eigenstates of $H_0$ and $H_0+V$.

mike stone
  • 58,971
  • 4
  • 53
  • 158
1

Note that your plot assumes that $V_{if}$ is non-zero. This is telling you that if the perturbation connects degenerate states (such that $\omega_{if} = E_f-E_i$ is zero and $V_{if}\neq 0$), then the transition between these states is favoured over the others.

The transition to other states would cost more energy (than zero) so it is less likely.

If the perturbation is diagonal in the degenerate subspace, or if there is no degeneracy, then there are no $\omega_{if}$ and $V_{if}$ that satisfy the conditions above simultaneously.

Lucas Baldo
  • 1,918