Electric field component in a capacitor with dielectrics inserted partially

Question

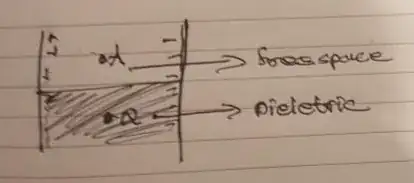
In the above set up I have two oppositely charged capacitor plates seperated by a distance 'd' with half of the region between filled with a dielectric material of constant $K$ and the other half in vacuum. My question is how would we prove that in both regions, the electric field is normal to the surface of plate at all points?

The context for the above is that I am trying to understand this answer which proves that the electric field is same in the dielectric media and the free space regions. It assumed that electric field only exists in direction normal to surface in region between plates and I'm trying to justify that.

Answer 1

My question is how would we prove that in both regions, the electric field is normal to the surface of plate at all points?

The electric-static field is always normal to the surface of a conductor at the conductor. But you want to know why it is normal to the plates between the plates. Unfortunately, you won't find a rigorous mathematical proof of that, because it is not rigorously mathematically true. It is approximately true. It is true to a very good approximation, but it is not exactly true. The field lines actually bulge a little away from center. The effect is small toward the center of the plates, but gets larger toward the edges. This bulging is generally called "fringe" effects.

Practical capacitors are designed to have minimal space between the plates. So, the ratio between plate area to plate spacing is very large. When this ratio is very large, fringe effects are usually neglected, i.e. treated as nonexistent.