$\hat{IR}$ refers to the unit vector denoting the incident ray unit vector $\hat{RR}$ refers to the unit vector denoting the refracted ray unit vector $\hat{N}$ refers to the unit vector denoting the normal unit vector
Things that I know about cross product: $\overrightarrow{A} \times \overrightarrow{B} = AB\sin\theta$.
Snell's law in vector form
I referred to this link but I can't understand any of the explanations about how we can arrive to the cross product form of Snell's Law
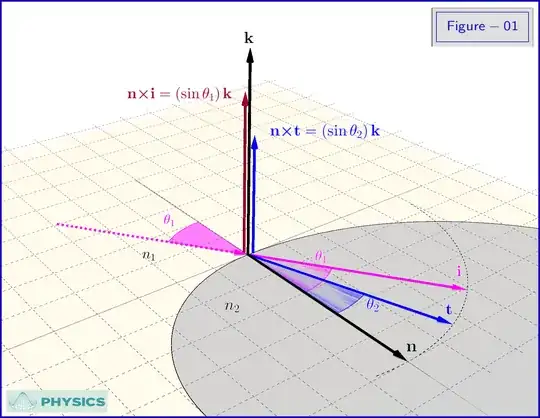
Notation in Figure-01 : \begin{align} n_1,n_2 & \boldsymbol{=} \texttt{indices of refraction} \nonumber\\ \theta_1,\theta_2 & \boldsymbol{=} \texttt{angles of incidence and transmission} \nonumber\\ \mathbf i & \boldsymbol{=} \texttt{unit vector on incident ray} \nonumber\\ \mathbf t & \boldsymbol{=} \texttt{unit vector on transmitted ray} \nonumber\\ \mathbf n & \boldsymbol{=} \texttt{unit vector normal to the interface of the two media} \nonumber\\ \mathbf k & \boldsymbol{=} \texttt{unit vector normal to the plane of }\mathbf i,\mathbf t,\mathbf n \nonumber \end{align}
Snell's law is expressed as
\begin{equation}
n_1\sin\theta_1\boldsymbol{=}n_2\sin\theta_2
\tag{01}\label{01}
\end{equation}
or
\begin{equation}
\sin\theta_2\boldsymbol{=}\mu\sin\theta_1\,,\qquad \mu\boldsymbol{=}\dfrac{n_1}{n_2}
\tag{02}\label{02}
\end{equation}
so
\begin{equation}
\underbrace{\left(\sin\theta_2\right)\mathbf k}_{\left(\mathbf n\boldsymbol{\times}\mathbf t\right)}\boldsymbol{=}\mu\underbrace{\left[\left(\sin\theta_1\right)\mathbf k\right]}_{\left(\mathbf n\boldsymbol{\times}\mathbf i\right)}
\tag{03}\label{03}
\end{equation}
that is Snell's law in vector form
\begin{equation}
\left(\mathbf n\boldsymbol{\times}\mathbf t\right)\boldsymbol{=}\mu\left(\mathbf n\boldsymbol{\times}\mathbf i\right)
\tag{04}\label{04}
\end{equation}
