Law of refraction in vector form: how is this derived?

Question

I am told that the law of refraction can be stated in the following two parts:

1. $\mu_1 \sin(\theta_i) = \mu_2 \sin(\theta_r)$
2. The incident ray, the normal to the surface separating the media at the point of incidence, and the reflected ray lie in one plane.

I am then told that both parts of the law can be put into vector form as

$$\vec{n}_2 = \vec{n}_1 - (\vec{n}_1 \cdot \vec{s}) \vec{s} + \left( \sqrt{(\mu_2)^2 - (\mu_1)^2 + (\vec{n}_1 \cdot \vec{s})^2} \right) \vec{s}, \tag{1.2}$$

where $\vec{n}_1$, $\vec{n}_2$, and $\vec{s}$ are the unit vectors of the incident ray, the reflected ray, and the normal to the surface, respectively, and $\theta_i$ and $\theta_r$ are the angles of incidence and refraction, respectively. The refractive indices of the two media are $\mu_1$ and $\mu_2$, and the incident ray is in the medium of refractive index $\mu_1$.

I don't understand exactly how (1.2) was derived. How is this derived from the two parts of the law of refraction? Please show this carefully, so that I can follow.

---

EDIT

Answer 1

Given two vectors $\vec a$ and $\vec b$, the vector projection of $\vec a$ onto $\vec b$ is:

$$\vec a_{\parallel \vec b}= \frac{\vec a \cdot \vec b}{\vec b \cdot \vec b} \vec b$$

The component of $\vec a$ that is perpendicular to this is called the vector rejection on $\hat b$:

$$ \vec a_{\perp \vec b}=\vec a - \vec a_{\parallel \vec b}=\vec a - \frac{\vec a \cdot \vec b}{\vec b \cdot \vec b}\vec b $$

If $\vec b=\hat b$ is a unit vector:

$$ \vec a_{\perp \vec b}=\vec a -(\vec a\cdot \hat b)\hat b$$

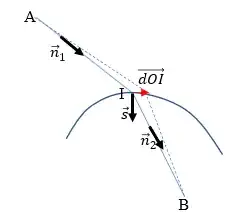
Armed with that geometric knowledge we can address the question. We can capture the index of refraction and wave direction with the wave vector:

$$\vec k_{\alpha}=\mu_{\alpha}\hat n_{\alpha} $$

(with $\alpha\in(i, 1)$ or $\in(r, 2)$).

The fact that the phases of the incident and refracted rays need to match along the boundary (perpendicular to $\vec s$) means that wave vector rejection onto $\hat s$ is continuous across the boundary:

$$\vec k_{r,\perp \hat s} = \vec k_{i,\perp \hat s}$$

or

$$\mu_2 \vec n_{r,\perp \hat s} = \mu_1 \vec n_{i,\perp \hat s}$$

which is Snell's Law.

From here, you go in two directions. First:

$$\vec n_{r,\perp \hat s} = \frac{\mu_1}{\mu_2} \vec n_{i,\perp \hat s}= \frac{\mu_1}{\mu_2}[\hat n_i-(\hat n_i\cdot \hat s)\hat s] $$

solves for the transverse component of the unit vector of the refracted wave $\hat n_r$, which can be written:

$$\hat n_r = \left(\begin{array}{c} n_{r,\perp \hat s} \\ n_{r,\parallel \hat s}\end{array}\right)$$

Here, the 3rd dimension (along $\hat n \times \hat s$) has been suppressed. The remaining basis vectors are in the $n-s$ plane, with $\left(\begin{array}{c}0\\1\end{array}\right)=\hat{s}$ and $\left(\begin{array}{c}1\\0\end{array}\right)$ along $ (\hat n\times\hat s)\times \hat s$.

Sin $\hat n_r$ is a unit vector:

$$ ||\hat n_r||^2 = n_{r,\perp \hat s}^2 + n_{r,\parallel \hat s}^2=1 $$

so that:

$$\hat n_r = \left(\begin{array}{c} n_{r,\perp \hat s} \\ \sqrt{1-n_{r,\perp \hat s}^2}\end{array}\right)$$

We have a vector expression for the transverse component. Note that:

$$ \left(\begin{array}{c}0\\1\end{array}\right)=\hat s$$

so the vector expression for the longitudinal component is:

$$ \vec n_{r,\parallel \hat s}= \sqrt{1-n^2_{r, \perp\hat s}}\hat s $$

Add those together to get:

$$\hat n_r = \frac{\mu_1}{\mu_2}[\hat n_i-(\hat n_i\cdot \hat s)\hat s] + \sqrt{1-n^2_{r, \perp\hat s}}\hat s$$

and substitute:

$$\hat n_r = \frac{\mu_1}{\mu_2}[\hat n_i-(\hat n_i\cdot \hat s)\hat s] + \sqrt{1- \left\Vert\frac{\mu_1}{\mu_2}[\hat n_i-(\hat n_i\cdot \hat s)\hat s] \right\Vert^2}\hat s$$

and turn the crank.

Comment on notation: Note that all $\hat n_{\alpha}$ are unit vectors. The projection or rejection of that onto another vector $\vec v$ is not necessarily a unit vector, and hence, does't have a hat. So the arrow over the $n$ in $\vec n_{r,\parallel \vec v}$ refers to the resultant vector after vector projection onto $\vec v$, even though the initial vector, $\hat n_r$, was a unit vector.

Meanwhile, the operation of scalar projection/rejection, has neither, e.g. $a=n_{r,\parallel \vec v}$ is a scalar which can converted into a vector a la:

$$\vec n_{r,\parallel \vec v} = a\hat v$$

Answer 2

Denote by $\mathrm{A}$ the point of departure, $\mathrm{B}$ the point of arrival of the ray, and $\mathrm{I}$ the point of contact with the refracting surface. The optical path is $L = \mu_1 \mathrm{AI} + \mu_2 \mathrm{IB}$.

Fermat’s principle tells us that this path is extremal with respect to a small displacement $\overrightarrow{d\mathrm{OI}}$ tangent to the surface of the refracting surface.
At the first order in $\overrightarrow{d\mathrm{OI}}$, it is not difficult to show (see below!) that $d(\mathrm{AI}) = \vec{n_1} \cdot \overrightarrow{d\mathrm{I}}$ and $d(\mathrm{IB}) = -\overrightarrow{n_2} \cdot \vec{d\mathrm{OI}}$ with $\vec{n_1}$ and $\vec{n_2}$ globally from $\mathrm{A}$ to $\mathrm{B}$. So, to the first order:

$$dL = {(\mu}_1\vec{n_1} - \mu_2\vec{n_2}) \cdot \overrightarrow{d \mathrm{OI}} = 0$$

As $\overrightarrow{d \mathrm{OI}}$ is any displacement in the tangent plane, this means that $ {(\mu}_1 \vec{n_1} - \mu_2 \vec{n_2}) = \alpha\vec{s}$.

We then write $\mu_2 \vec{n_2} = -\alpha \vec{s} + \mu_1 \vec{n_1}$ and we square it, the vectors being unitary: ${\mu_2}^2 = \alpha^2 - 2\alpha \mu_1(\vec{n_1} \cdot \vec{s}) + {\mu_1}^2$.

It is a quadratic equation whose solutions are: $\alpha = \mu_1(\vec{n_1} \cdot \vec{s}) \pm \sqrt{{\mu_1}^2{(\vec{n_1} \cdot \vec{s})}^2 - ({\mu_1}^2 - {\mu_2}^2)}$.

If $\mu_1 = \mu_2$, we must find $\vec{n_1} = \vec{n_2}$ and therefore $\alpha = 0$. So we keep: $\alpha = \mu_1(\vec{n_1} \cdot \vec{s}) - \sqrt{{\mu_1}^2{(\vec{n_1} \cdot \vec{s})}^2 - ({\mu_1}^2 - {\mu_2}^2)}$. Hence finally:

$$\mu_2\vec{n_2} = \mu_1\vec{n_1} - \mu_1 \left( (\vec{n_1} \cdot \vec{s}) - \sqrt{{\mu_1}^2{(\vec{n_1} \cdot \vec{s})}^2 - ({\mu_1}^2 - {\mu_2}^2)}\vec{s} \right)$$

I can't find the same relationship as you? But by examining when the term under the root vanishes (limiting angle), I find a correct relation and therefore it is possible that your formula is incomplete?

Complement: To prove $d(\mathrm{AI}) = \vec{n_1} \cdot \vec{d \mathrm{OI}}$, it suffices to write $\mathrm{AI} = \sqrt{{\vec{\mathrm{AI}}}^2}$ and differentiate: $d(\mathrm{AI}) = \dfrac{\vec{\mathrm{AI}} \cdot d\vec{\mathrm{AI}}}{\sqrt{{\vec{\mathrm{AI}}}^2}} = \vec{n_1} \cdot \vec{d \mathrm{OI}}$ with $\vec{\mathrm{AI}} = \vec{\mathrm{OI}} - \vec{\mathrm{OA}}$ and $\mathrm{A}$ fixed.

Sorry for my poor english! English is not my native language.