Variation of Twin Paradox - Half Triplet Paradox

Question

Here is a variation of Twin Paradox. I call it Half (for bottom half of Twin Paradox) Triplet Paradox with no change of inertial frames involved. Consider this scenario. There are triplets T1, T2 and T3. At the Start point their clocks are synchronized. T1 and T3 stay put hence their world line is vertical. T1 and T2 are together at Start. T2 moves at constant velocity and ends up with T3 at End. Hence T2 has a diagonal world line. NOTE: In this scenario none of the triplets is switching any inertial frame (unlike in Twin Paradox case).

BTW can we simply replace the triplets with stopwatches and compare the recorded time by each between Start and End and the experiment still remains the same? And using synchronization using light beams we do not have to explain how T3 got to the distant point prior to the experiment Start.

Obvisouly T1 and T3 are not moving with respect to each other so they will see each other aging at same rate. This allows us to compare age of T1 with T2 at Start and T2 with T3 at End.

Questions:

• Between Start and End will T1 and T3 see T2 aging slowly as T2 is moving at constant velocity with respect to them? Conversly will T2 see T1 and T3 aging slowly because they are moving at constant velocity away and towards T2?

• At End will T1 and T3 have aged more that T2?

  • If so why? Why is T2's aging different that T1 and T3's.
  • If not? Why not? What is different about this qualitatively from the Twin Paradox?

Does the answer simply boil down to how Minkowski Metric works in SR? But why does it work like that?

Answer 1

UPDATE:
I noticed the first sentence and wanted to make a comment on it.

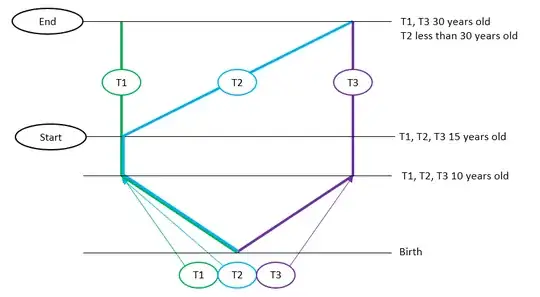
Here is a variation of Twin Paradox. I call it Half (for bottom half of Twin Paradox) Triplet Paradox with no change of inertial frames involved.

In the scenario you described the three travelers T1, T2, and T3 from "birth" to "end" are non-inertial. Although they are piecewise-inertial, any kink in the worldline renders the traveler non-inertial [since a ball on a frictionless table in their ship will move at the kink event]. Only a traveler with a forever-straight worldline on a spacetime diagram (like one that could be drawn in the lab frame below) is inertial.
If you restrict consideration to the portion between "start" and "finish", then they are inertial.

---

Here's a spacetime diagram on rotated graph paper
so that we can more easily read off the ticks.
The light-clock diamonds are traced out by the light-signals in an observer's light clock.
The area of all light-clock diamonds are equal, in accordance with the principle of relativity.

I've done my best to try to model the OP's scenario.

In the following, each diamond (1 tick) represents 2.5 years.

The speeds at the initial separation are $|v|=5/13$, which corresponds to time-dilation factor $\gamma=\frac{13}{12}\approx 1.0833$, and Doppler factors of $k=\pm 3/2$ (rational $k$'s are associated with Pythogorean triples, which make the arithmetic simpler).

[$k$ is an eigenvalue of the Lorentz boost and describes the reshaping of the light-clock diamond, by stretching by $k$ in the forward direction and shrinking by $k$ in the backward direction, preserving the area. (Recall the determinant of a boost is 1 and the eigenvectors are along the light cone.)]

---

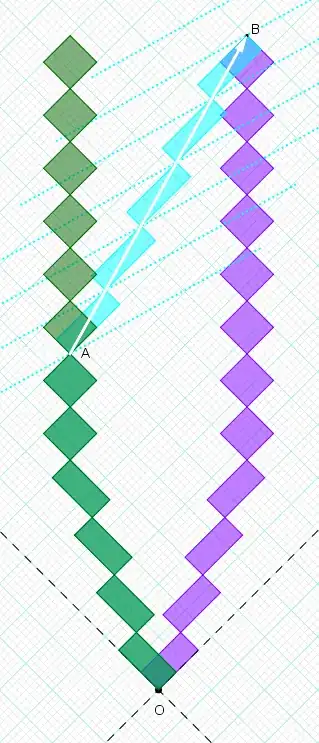
You can count the ticks (each representing 2.5 years) along these piecewise-inertial worldlines.

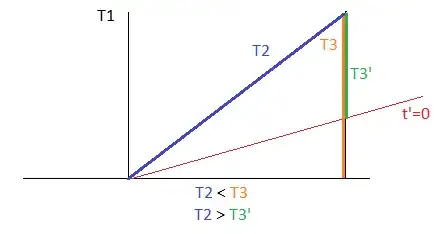
T2 traveled at (5/9)c in order to meet T3 at T3's 30th birthday.
The lab-coordinates of events A and B are $A=(t=6.333,x=-1.666)$ and $B=(t=12.333,x=1.667)$.
T2's last leg has $\Delta x=10/3$ ticks and $\Delta t=6$ ticks in this frame.
( $\gamma=\frac{1}{\sqrt{1-v^2}}=\frac{9}{2\sqrt{14}}\approx 1.20267$. So, $(6/\gamma)=\frac{4\sqrt{14}}{3}\approx 4.9888$.)

Thus, T2 elapsed $\sqrt{6^2-(10/3)^2}=\sqrt{224/9}\approx 4.9888 $ ticks = $12.4722$ years.
So, T2 is $15+12.4722=27.4722$ years old when T2 meets T3 at T3's 30th birthday.
A lab observer who is at rest and meets event B has age 12.333 ticks $\approx 30.8333{\rm\ years}$.

I've drawn in T2's lines of simultaneity, which are parallel to the spacelike diagonals of T2's diamonds.

Note that 4 ticks after T1 and T2 separate:

• T1 says "when 4-ticks on T1's clock have elapsed, T2 has not yet elapsed 4-ticks on T2's clock"
• T2 says "when 4-ticks on T2's clock have elapsed, T1 has not yet elapsed 4-ticks on T1's clock"

(For an elaboration of the symmetry of time-dilation, refer to my answer https://physics.stackexchange.com/a/383363/148184
in How can time dilation be symmetric? )

These diagrams are based on methods described in my paper
"Relativity on Rotated Graph Paper"
Am. J. Phys. 84, 344 (2016) https://doi.org/10.1119/1.4943251 ( early draft: https://arxiv.org/abs/1111.7254 )

See also https://www.physicsforums.com/insights/relativity-rotated-graph-paper/

In addition, I mentioned Twin paradox problem from a perverse perspective in the comment to the OP.

Yes, this situation is due to Special Relativity.
These diamonds are precisely traced out by the associated light clocks, which are constructed according to the principle of relativity and the constancy of the speed of light.
From this construction visualized on a spacetime diagram, one can likely come up with all sort of valid ways of thinking about how these results occur (e.g. time dilations, length-contractions, doppler effects, Lorentz transformations, etc...).
Why is it like this?
This is our universe as we understand it, and is well supported by a huge amount of experimental data.
The Galilean framework with absolute time and absolute length and its associated predictions are not supported by experimental data, especially at high relative speeds. Someday we may have super-high-precision watches where these effects can be measured at lower relative speeds.

Answer 2

It is both true that T2 is aging slower in the frame of T1 and T3 and that T1 and T3 are aging slower in the frame of T2.

It is also true that when T2 and T3 meet, T2 will have aged less than T3.

How does this reconcile with the fact that T2 thinks the others are aging slower, are they just wrong? Actually, all ths is possible due to the relativity of simultaneity.

Notice that in a Lorenz transform, we transform the time variable:

$$ t' = \gamma (t - v x/c^2) .$$

This means that the starting point in the T2 frame, $t'=0$, is a tilted line in the original frame:

$$ t = v x / c^2 $$

What this essentially means is that in the T2 frame, T3 started its clock too early, and should have started it at a later time to be fair, and that's the only reason that more time has passed for T3. If T3 had started its clock when $t' = 0$, then indeed less time would have passed for T3 (T2 < T3' in the figure), because it is moving with a relative velocity to T2.

Answer 3

I should start by saying that:

1. The two lower layers of your diagram are irrelevant- all that counts is the top layer where T2 moves relative to T1 and T3.

2. You make a misleading assumption when you say that the clocks of T1, T2, and T3 are all synchronised. I will explain this below.

The answers to your questions are as follows...

Yes, as measured by T1 and T3, T2's clock will seem to run slow, whereas in T2's frame of reference, T3's clock will seem to be running slow. The effects are entirely reciprocal.

Yes, as measured by T1 and T3, T2 will seem to have aged less than they have over the course of T2's journey. However, T2 will consider that T3 has aged less over the course of T3's journey. There is no contradiction here, but to see that there is no contradiction you must remember to take into account the fact that T2 and T3 disagree about when their respective journeys began. Both T1 and T3 believe that T2 started her journey at time T=15years. However, in T2's frame of reference, T3 began her journey at a time later than T=15years. You have mistakenly assumed that because T2 set her clock to be the same as T1's, and because T1's was synchronised with T3's, then T2's was synchronised with T3's, when it was not. T=15years on T3's watch is not simultaneous with T=15years on T2's watch from T2's perspective.

If you have any difficulty following this, I suggest you take a simple analogy with lengths. Imagine T1 adopts one reference frame and T2 adopts another which is tilted at 45degree. T1 and T2 now each hold up a 1m stick vertically from ground level in their respective frames. Now ask yourself how 'tall' the sticks appear in each of the two reference frames. T1 will say that T2's stick is less tall than theirs because it is tilted over. However, T2 will believe that its stick is taller because the other stick is tilted over. Each thinks the other stick is less tall because it is tilted over. There is no contradiction, we are just seeing different points of perspective.

Answer 4

In the first part, we can assume that two distant stars at opposing distances were colonized by humans in previous trips, so clocks and calenders there are synchronized to the earth time.

When the twins arrive at their first destiny, if their own clocks show 10 years have passed, the destiny calender shows more than that. If their speeds were constant and equal, they now can syncronize their clocks with the stars clocks. As time goes by, they add more years over the 10 that they experience during the first trip.

When T2 meets T3 at the end of the second trip, his clock shows less time than T3 clocks. One easy way to understand it is to realize that the distance between T1 and T2 is smaller for him (length contration) than what is measured by T1 and T2. As both agree about the velocity of the ship, the time must be shorter for T2.

During the trip, it is true that T1 and T3 are aging slower than him (after all, they are moving in T2 frame). But as soon as he departs from T1 with velocity $v$, T3 is no longer syncronized to T1 for him. According to Lorentz transformation: $$t_3 = \gamma(t_2 - \frac{-v}{c^2}x_3)$$$$t_1 = \gamma(t_2 - \frac{-v}{c^2}x_1)$$ (according to T2 frame, T1 and T3 are moving with velocity $-v$). As his distance $x_3$ to T3 is different from his distance $x_1$ to T1 (that is zero at the start instant), those clocks are no longer syncronized for his frame.

In reality, as soon the T2 trip starts, the clock of T3 shows for him a future time, compared to T1. As he approaches destiny, while T3 clock ticks all the time slower for him, T3 clock still will show a bigger time, compared to his calender.