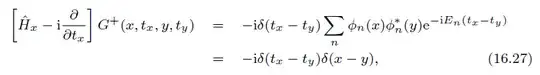I have a propagator
$$ K=\sum_k\langle x|a_k\rangle\langle a_k| y\rangle \exp\left\{ \frac{-iE_k(t-t_0)}{\hbar} \right\} ~~,\tag{1} $$
which I know satisfies the time-dependent Schrodinger equation
\begin{align} i\hbar\dfrac{\partial}{\partial t}K=\hat HK~~. \end{align}
I am only interested in the retarded propagator so I multiply it by the Heaviside function $\Theta(t-t_0)$. This enforces the condition that the probability density at time $t_0$ will diffuse only into the future. Therefore, I solve
\begin{align} i\hbar\dfrac{\partial}{\partial t}\Theta K&=\hat H\Theta K\\ i\hbar\left(K\dfrac{\partial}{\partial t} \Theta + \Theta\dfrac{\partial}{\partial t} K \right)&=\hat H\Theta K\\ i\hbar\, K\delta(t-t_0) &=\hat H\Theta K- i\hbar\,\Theta\dfrac{\partial}{\partial t} K ~~. \end{align}
Since the $\delta$-function picks out $t=t_0$, I can simplify $K$ on the LHS using (1) to write
\begin{align} \lim\limits_{t\to t_0}K&=\sum_k\langle x|a_k\rangle\langle a_k| y\rangle \exp\left\{ \frac{-iE_k(t_0-t_0)}{\hbar} \right\} \\ &=\sum_k\langle x|a_k\rangle\langle a_k| y\rangle \\ &= \langle x| y\rangle \\ &= \delta^{(3)}(\vec x-\vec y) ~~, \end{align}
which yields
\begin{align} i\hbar \,\delta(t-t_0) \delta^{(3)}(\vec x-\vec y) =\Theta \left(\hat H- i\hbar\dfrac{\partial}{\partial t}\right)K ~~. \end{align}
Now I see that $K$ is the Green's function for the given linear operator. However, in Sakurai's Modern QM, 3rd Ed. (p110), he has a minus sign on the $i\hbar$ on the LHS. Where does it come from?
This question is similar but does not explain where the minus sign comes from.