It is well-known that a hydrogen atom in free space prepared in an excited state, for example $\left| 2p_y \right\rangle$, will over time decay into the ground state $\left| 1s \right\rangle$. If not perturbed by any measurement of the atom or the emitted photon it will undergo an evolution through a superposition of the excited and ground state $$A(t) \left| 1s \right\rangle + e^{-i \omega t} B(t) \left| 2p_y \right\rangle$$ which leads to an oscillatory movement of the charge density along the $y$-axis. See for example this answer or this applet. This oscillating dipole causes the emission of a photon with a polarization given by the orientation of the dipole ($\hat{E} = \hat{d} = \hat{y}$ in this case).
This principle also applies to molecules, just with more complicated orbitals. Unlike the hydrogen atom they aren't spherically symmetric, hence the dipole moment is given by the geometry of the molecule. If you know how a molecule is embedded in a crystal you also know the polarization of the photons emitted by it.
Things start to get more complicated when the excited molecule is forced to interact with its own radiation inside a Fabry-Pérot cavity. If the cavity is resonant with the molecule's transition, the emitted field builds up in the cavity. The relative phase between the field and the charge oscillation is such that the molecule transfers energy to the intracavity field, making the molecule decay to the ground state faster than in free space. This is similar to stimulated emission, just that here one part of a photon triggers the emission of another part. [There is also a less intuitive explanation of the Purcell effect via the density of final states, for reference see Mark Fox – Quantum Optics: An Introduction chapter 10.]
My question is about the case when the cavity mode dictates the polarization of the field. This happens for example if there is a birefringent crystal in the cavity, see for example Wang et al. PRX 7(2) 021014 (2017). Light polarized along the fast axis of the crystal sees accumulates a different round trip phase than light polarized along the slow axis. Therefore the resonance frequency for the these two polarization eigenmodes is different.
Now imagine the following situation: The cavity mode with polarization along the fast axis (= $y$-axis here) is resonant with the $\left| e \right\rangle \to \left| g \right\rangle$ transition of the molecule, but the transition dipole moment of the molecule is not aligned with the cavity mode polarization:
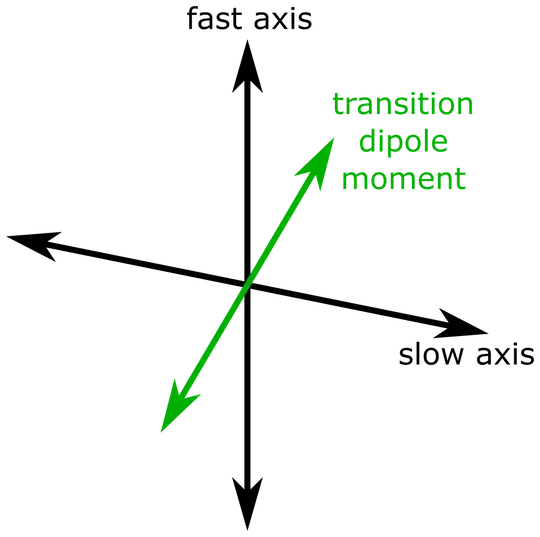
There is a correction factor $\xi^2 = \left| \hat{E} \circ \hat{d} \right|^2$ for the Purcell factor $F_{\text{P}}$ (equation 10.35 in Mark Fox' book) which takes this into account, but it doesn't talk about how the charges oscillate. I could imagine two different possibilities, both not convincing me:
- The charge density starts oscillating along the dipole axis. The field of the cavity mode (polarized along $y$-axis) builds up and decelerates the charge movement. But it can only decelerate the movement along the $y$-axis. The $x$ component is dampened as weakly as in free space. So after some time the movement becomes elliptical and finally parallel to the $x$-axis.
What I don't like about this scenario is that it would involve additional orbitals to explain the motion off the $\vec{d} = \left\langle e | \vec{x} | g \right\rangle$ axis, hence involving other orbitals, which have completely different energies. Furthermore the molecule would reach the ground state after measureably longer time, because the oscillation along the $x$-axis decays as slow as without cavity.
- The charge density moves only along the $y$-axis from the beginning, which means the field dampens the full movement of the charge density.
This situation also requires additional orbitals. Furthermore it assumes that the molecule knows about its environment already at the start of the emission and adjusts its behavior accordingly.