The question is:
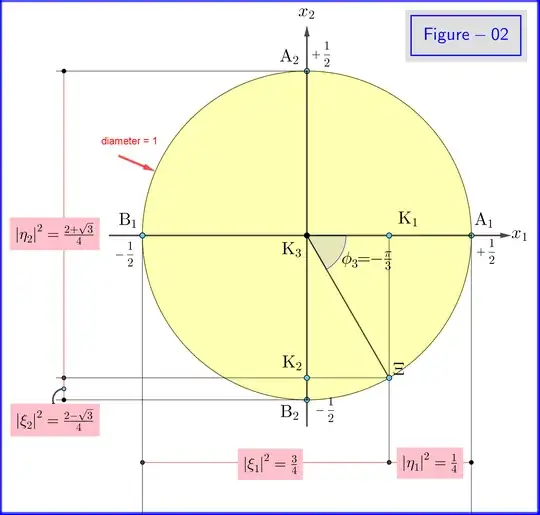
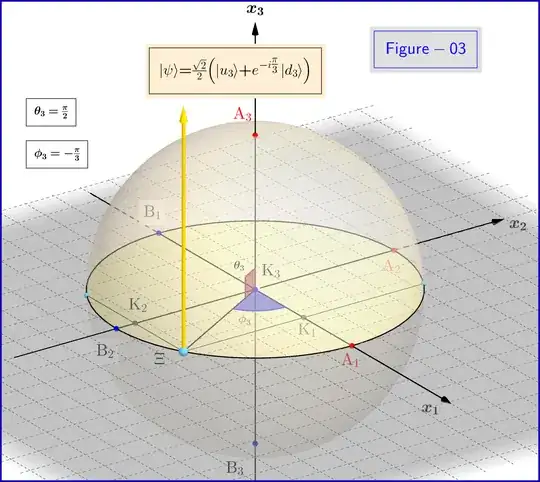
The angular momentum components of an atom prepared in the state $|\psi\rangle$ are measured and the following experimental probabilities are obtained: \begin{equation} P(+\hat{z}) = 1/2, P(−\hat{z}) = 1/2, \end{equation} \begin{equation} P(\hat{x}) = 3/4, P(−\hat{x}) = 1/4, \end{equation} \begin{equation} P(+\hat{y}) = 0.067, P(−\hat{y}) = 0.933. \end{equation} From this experimental data, determine the state $|\psi \rangle$. Note that in performing the measurements, the state $|\psi \rangle$ is prepared again and again.
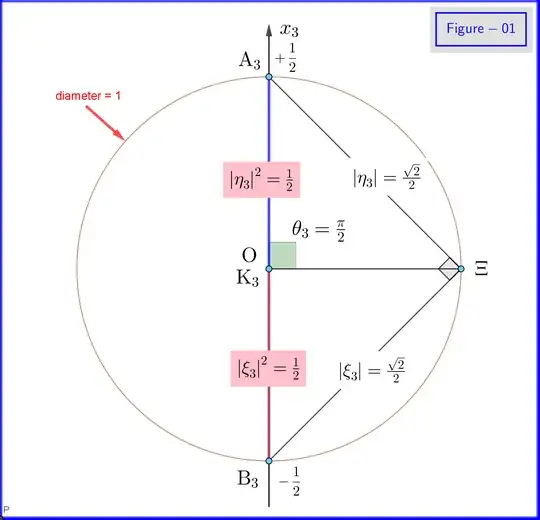
My attempt: $$ P(+\hat{z}) = 1/2 = P(−\hat{z}) $$ $$ |\langle {\uparrow}_z|\psi\rangle|^2=1/2 =|\langle {\downarrow}_z|\psi\rangle|^2 $$ $$ |\psi \rangle =\alpha |{\uparrow}_z\rangle+ e^{iδb} \beta|{\downarrow}_z\rangle $$ $$ |\langle {\uparrow}_z|\psi\rangle|= \alpha = 1/\sqrt(2). $$ Similarly, $$ |\langle {\downarrow}_z|\psi\rangle|= \beta = 1/\sqrt(2). $$
However, I don't know how to find $e^{iδb}$ term. Could someone please give a hint?