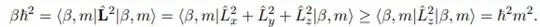I am comfortable with the argument that in order for the wavefunction to be single valued/2$\pi$ invariant this means that $L_z$ must be an integer value of $\hbar$.
$$U(2\pi e_z)=e^{-(2\pi i/\hbar)\hat L_z}=1$$
However I don't know how it follows from this that $|L|^2 = \beta \hbar^2$ where $\beta$ in an integer. $L_x$ and $L_y$ are indetermined so it seems fishy to say 'if' they were measured they would have integer $\hbar$ values and so $L_x^2 + L_y^2 + L_z^2$ would be an integer $\hbar^"$ value, since we can never actually measure all of these at once.