Why does a floating object displace more substance than a sunk object?

Question

Consider a box floating on water having a coin on top, now suppose after some time by some external influence, the coin is dropped into water. After doing the calculations, to my surprise, I found that the water level actually drops...I just can't understand this phenomena. For what reason does this happen? I think that my whole conception of buoyancy is wrong after this because intuitively I think water level rises because the coin would apply both it's weight and take up some volume while in the water.

---

Notes for future answers/ existing answers:

• After some deep thinking, I started to realize the problem was that I had this intuition that water would have been compressed by the weight somehow. How exactly does that effect vary in the scenario displayed above?
• After even more deep thinking, how does the behaviour of fluid change as we relax/ impose the condition of compressibility ? specifically how would results in this case differ? ( A diagram would be nice)
• Suppose we constantly applied a force onto the surface of a water, like a pressure, by the logic given in most answers, the water level should rise! but, intuitively it is often said that water level drops as we apply more pressure on the face open to atmosphere

---

My question is different from this stack because my confusion is mostly about the actual structure of the fluid and response of fluids to load rather than the directly calculated volume changes.

Answer 1

When submerged, the coin displaces as much water as it has volume (logical).

When floating on the box, the coin displaces as much water as corresponds to its weight.

As metal has a higher density than water, it means that the coin in the box displaces more water than when the coin is submerged.

Answer 2

The coin is denser than water. When placed on the box, it will displace it's weight in water, which is more volume than the coin. When placed directly in the water it will sink to the bottom and displace only it's own volume in water, which will be less because it's denser.

Another way to think about it is to have a platform below the box open to the water and a coin on the bottom of the tank. If you place the coin on the platform, it will pull the box down and displace more water than when it was on the bottom of the tank. It will actually displace the same amount of water as if you put it on top of the box.

Answer 3

The key is that the box can bob up and down. If both were completely submerged to begin with, then you'd be right: no rearranging of them underwater will cause some sort of strange change in displacement. But because the box is floating, so that not all of it is displacing water, the amount of water it displaces can change if it moves up or down, thus bringing relatively more or less box into the water.

When your coin falls off, the box bobs slightly up, which reduces the amount of water it displaces.

Hence, the water level falls.

(Note: actually, you need a bit more quantitative analysis to see it will fall, because technically we need to also account the change in displacement of the water when the coin enters it now which will compete against the bobbing to see that the latter will, in fact, win, but the point here is to show where and how, conceptually, the fall in water level can arise despite the seemingly "added displacement".)

Answer 4

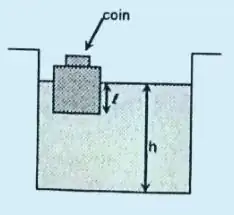
Based on the wording of your question as well as some of your comments, it seems as though you believe that the amount of liquid displaced by a submerged object is related to the weight of the object. It is not.

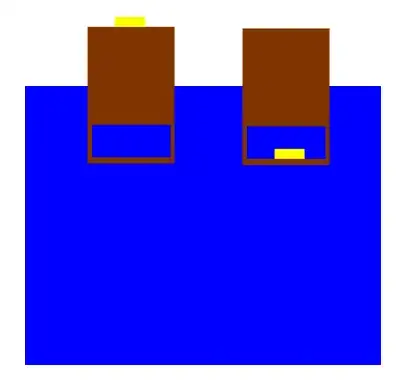
If a coin is submerged in water, it will always displace the exact volume of water that is equivalent to its own volume. Whether the coin is perfectly weightless or it weighs a million tons, the amount of water displaced will be the same as long as the volume of the coin is the same. Even if the coin was lighter than the water and was being held under the water by some force, the displacement would be the same. It also does not matter whether the coin is resting on the bottom, in the process of sinking, or glued to the side of the container as none of those factors are related to displacement at all.

In terms of the explanation for why the water level drops, since the water is less dense than the coin, when the coin is placed on top of the box the volume of water displaced is the amount of water which equals the weight of the coin. Compare that to when the coin is dropped in the water, during which time the amount of water displaced is the same as the volume of the coin only. Since the amount of water which equals the weight of the coin is greater than the amount of water which equals the volume of the coin, the amount of displaced water is greater when the coin is resting on the box.

This may have contributed to the confusion regarding the relationship between weight and displacement, but remember that the only reason weight matters when the coin is on top of the box is because its affecting how much of the box is pushed into the water. once the object is completely submerged, weight ceases to have any impact on displacement.

finally, this was briefly mentioned in a comment, but it may be easier to visualize whats happening if we exaggerate the parameters. Imagine if instead of a coin, we used a tiny metal cube made of some hypothetical material which is far heavier than any element but only takes up one cubic millimeter of volume. If we drop the cube into the water, exactly one cubic millimeter of water will be displaced. However, if we place it on the box then a huge portion of the box will sink under the surface, displacing far more than a cubic millimeter of water.

Edit based on the edit in the question: Under the majority of circumstances, water is, for all intents and purposes, incompressible. At the very last, the compressiblility of water can be ignored for problems like this. The fact that water does not compress is actually one of the big reasons why it is displaced upwards in the first place. When you place the box in the water, it can not compress so it must instead move somewhere else. In the case of this problem that "somewhere else" is upwards into the empty space at the top of the container.

Answer 5

I'm not an expert so please check if this makes sense.

It seems like the "reason" for this is that when it's on the box, it's displacing water "using" the box. Since the box is less dense, the same weight occupies more space, so the weight of the coin gets amplified by the ratio of its specific weight to the box's specific weight. For example, if the box's specific weight is 10 times lighter than the coin's, the coin will now be pushing on 10 times the volume as its own (- the coin's) volume into the water. (Ignoring the difference in water level. I'm just making the point that what is pushed is "box", not "coin".)