Why do photons follow the geodesic curvature of the gravitational field instead of the spacetime curvature?

Question

If mass merely 'curves' spacetime, why do photons follow the geodesic path of the gravitational field (path A) instead of the spacetime curvature itself (path B)?

It seems, as if, the gravitational field exerts a continuous pull of the space-time continuum, not a mere bend.

Given we are defining a behavior from an external frame of reference, the space-time 'bend' analogy comprises a 'localized' stretch of space as well as a 'localized' stretch of time, but does not seem to comprehend the gravitational 'pull'. I tend to imagine a spaceship traveling through a space-time grid at a constant acceleration of 1 g, I don't see it as 'bending' time or space, but 'pulling' through time and space.

In other words, I'm curious of why does it seem more appropriate to define the gravitational force exerted by any given mass (like a planet or a black hole) as a mere 'warp', 'bend' or 'curvature' of the space-time fabric instead of a continuous 'pull' of the space-time fabric itself. Isn't it the four-dimensional nature of gravity more akin to a continuous 'pull' of space-time fabric, rather than a tree-dimensional 'bend'?

My concern being the semantics getting in the way of a more comprehensive yet intuitive understanding of space-time and gravity.

For the purpose of this question, the gravitational field exerted by the celestial object is stronger than Earth.

Answer 1

The only possible answer that can be given here is that those gridlines are not an accurate representation of spacetime curvature. It's unfortunate, because we would all love to have a graphical way of understanding general relativity, but it's true. Therefore, it doesn't really make sense to draw conclusions based on it.

The -time part in spacetime curvature is essential. It's the most direct effect that gravity has on trajectories, because the geodesic equation can be rephrased as saying that objects move to maximize the time spend in their movement. Even if the gravitational field doesn't change with time, you can't just look at how space is curved and ignore time. And even if you could, space curvature is complicated, being described by the Riemann tensor, which has six components at each point. I don't think you can represent it by drawing curved gridlines.

Answer 2

I think the lines in the drawing describe the tidal deformation of a local cube, which is not the same as a geodesic.

Answer 3

B is merely an attempted depiction of the curvature of spacetime. A is an attempted depiction of the altered path of a mass or photon affected by the curve. Once a photon's path is altered it will continue on the altered course, it would not curve back away from the planet as spacetime is depicted to do.

Answer 4

See some graph depicting the four dimensional photon track in the spatial three:

This is a common approach to try to gain some visualization of the curvature of space-time by a gravitational mass. It starts by depicting space as a two-dimensional elastic sheet. If a massive ball is placed on this sheet, it will produce an indentation or curvature. If a smaller ball is rolled by the larger one, its path will be deflected by the indentation of the larger ball. While not adequate to depict the curvature of 4-dimensional space-time, it at least is a start.

In this graph time is inferred by the existence of a track . By definition light is following a geodesic, meaning :

In relativity: Curved space-time and geometric gravitation

…the shortest natural paths, or geodesics—much as the shortest path between any two points on Earth is not a straight line, which cannot be constructed on that curved surface, but the arc of a great circle route.

The word is extending the simple geometrical view "the shortest distance between two points is a straight line" . Extending this concept to the surface of a sphere, gives an arc. In the complicated four dimensional space of general relativity the concept produces geodesics, a four dimensional path. From the mathematics of light and zero mass particles, comes that they have to follow geodesics. One has to be careful in drawing conclusions from graphs used to approximate a complicated mathematical space.

The graph from the link is drawn knowing that photons are zero mass particles ( or that light follows geodesics) but the time component is in the duration of the path, not seen easily as the velocity is c.

Why do photons follow the geodesic curvature of the gravitational field instead of the spacetime curvature?

Photons are a probe of space-time curvature,because by the mathematics they have to follow geodesics. All particles follow a geodesic, except with the zero mass photons "plot" the curvature of space time about a given mass, since the effect on the energy momentum tensor of a single photon can be neglected with respect to a massive star.

Geodesics are commonly seen in the study of Riemannian geometry and more generally metric geometry. In general relativity, geodesics in spacetime describe the motion of point particles under the influence of gravity alone. In particular, the path taken by a falling rock, an orbiting satellite, or the shape of a planetary orbit are all geodesics in curved spacetime. More generally, the topic of sub-Riemannian geometry deals with the paths that objects may take when they are not free, and their movement is constrained in various ways.

Answer 5

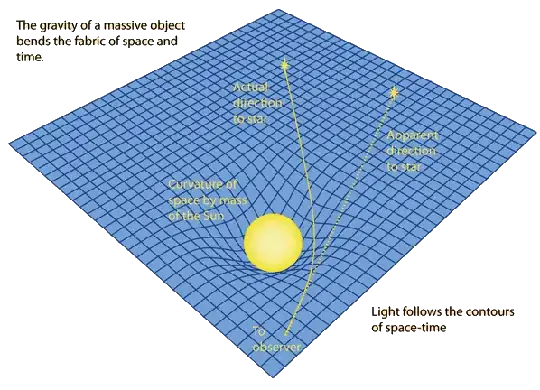
As stated in other answers, the gridlines presentation is highly problematic.

The problem is that it has no way of accomodating range of velocity. How much the trajectory of an object is curved is also dependent on the velocity of the object.

There is another model of gravitational interaction that does accomodate that. It's called the river model

Imagine all of space is a river that is flowing from higher gravitational potential to lower gravitational potential. Except: all objects in that river are not co-moving with the velocity of that river (there is no such thing as measuring the velocity of that river). What does happen is that objects in that river will co-accelerate with the river.

This river model accomodates the orbits of the planets around the Sun.

Next imagine an object that is on a hyperbolic trajectory. (for example the object Oumuamua.) The point nearest to the Sun of Oumuamua was at about 0.25 Astronomical Units. But the trajectory of Oumuamua is curved much less than that of the planet of the solar system because Oumuamua is moving much faster than the planets of the solar system.

About gravitational deflection of light.

Gravitational deflection is a single phenomenon, but for the purpose of exposition it is possible to discuss time aspect and spatial aspect separately.

For geometically flat spacetime we have a value for the ratio of volume and surface area of a sphere.

Curvature of space has the property that this ratio comes out differently. How much different? That is calculated in the answer to the question: how much does the curvature of space change the volume of Earth by?

(So you see that when people try to represent space curvature with something like gridlines they have to use ginormous exaggeration.)

How propagating light is affected:
A propagating wave front is negotiating all of space. In a gravitational field there is a gradient of higher to lower potential. This gradient has the same effect as the gradient in a medium where the propagation of light is not uniform.

(Example of medium with non-uniform propagation of light. Optical fibers have a slightly different composition from core to perimeter. Closer to the perimeter the light propagation is a bit faster. Light that deviates from travelling along the core is refracted back to the core.)

The spatial aspect of gravitational deflection of light accounts for about half the total deflection.

The time aspect accounts for the other half. In 1907 Einstein published an exploratory theory that featured gravitational time dilation, but not curvature of space. One implication of that exploration was that light propagating down a gravitational gradient will display a shift of frequency. (In 1959 the Pound-Repka experiment confirmed this.) The other implication of the 1907 exploration was deflection of light by a gravitational field. The amount of deflection on the basis of that exploratory idea is about half of the deflection predicted by General Relativity.

So:
It's only when you are all the way up to the speed of light that the time aspect and the spatial aspect of spacetime curvature are equal contributors to the total effect.

At lower velocities, such as the velocities of the planets, the contribution of the spatial curvature is generally negligable.

Reminder:
The curvature of spacetime is a single thing. Separating in time aspect and spatial aspect is unnatural, but for the purpose of exposition it has its uses.

[Later edit]

It may be that you are wrongfooting yourself by holding on to visualizations that involve concepts such as 'pulling'.

My favorite: a visualization in the form of a slowly rotating Ehrenfest disk.

Construct a space station that is large enough and with such an angular velocity that inhabitants of that Ehrenfest disk at a particular distance ‘r’ to the axis of rotation experience 1 G of centripetal acceleration.

If you take the stairs to one level higher you find that for a clock on that higher level a bit more proper time is elapsing. Go to a shaft, and release an object. You know that once released the object will continue along an inertial trajectory. The motion of the object with respect to the Ehrenfest disk is accelerated motion.

Do the Pound-Rebka experiment onboard that rotating space station. If you do that experiment with the same 1 G of acceleration the outcome is the same as on Earth. Same acceleration, same outcome.

Crucially:
The logic of GR does not extend beyond that.
GR does not attempt to explain gravitational interaction beyond that. This is a 'choose your battles' situation. You push to whatever point you can still say meaningful things, and at that point you stop.

On the Ehrenfest disk the Minkowski metric describes the relation between time and space. If you go up the stairs time and space both change (a tiny amount), as described by the Minkowski metric. The change of time and the change of space are so interconnected it is better to think of the change as a single conversion.

In GR spacetime the GR metric describes the relation between time and space. As you move up and down a gravitational potential both time and space change (a tiny amount). It is better to think of that change as a single conversion. Likewise it is better to think of the mediator of gravitatonal interaction as a single feature: curvature of spacetime.