I realize this isn't possible, but I can't see why not, especially if you change the model a little bit so that the balls simply travel through a tube of water on the way up, rather than exactly this model.
Please be clear and detailed. I've heard explanations like "the balls wouldn't move" but that doesn't do it for me - I really do not see why the balls on the right would not be pulled/pushed up, and the rest of the chain wouldn't continue on.
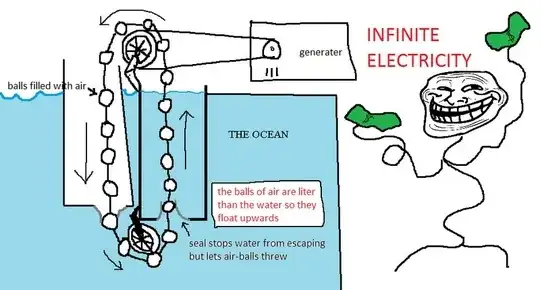
Let's follow one particular ball all the way around. The ball will enter the water well below the surface. The pressure there is much higher than at the surface, so we need to do a lot of work just to push the ball into the water. It's so much work that it cancels all the work that ball will do as it floats upward on the other side, giving no net work gained as the ball makes a complete circuit.
Let's see this mathematically. We can ignore the gravitational force on the ball since gravity pulls down as much as up as you traverse the loop; we will focus on just the buoyant force and the force needed to push the ball into the water.
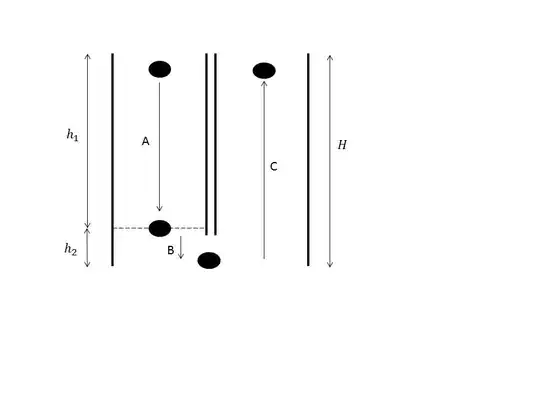
If the ball enters the water at depth $d$, the pressure is $g \rho d$ with $g$ gravitational acceleration and $\rho$ the density of water.
The work done to submerge the ball is then the pressure times its volume, or $$W_{\rm submerge \; ball} = g \rho V d.$$
The force upwards on the ball is the weight of the water it displaces, which is $g \rho V,$ and the work the water does on the ball as it floats upward is this force times the distance the ball floats upward, or $$W_{\rm buoyancy \to ball} = g \rho V d.$$
We can now see that $$W_{\rm submerge \; ball} = W_{\rm buoyancy \to ball},$$ meaning that as the ball goes around, we'll have to do just as much work on it as we will get back, so the ball doesn't give us any free energy in a complete loop.
The picture shows many balls, not just one. If we imagine the entire apparatus making a loop, though, each ball will make one full loop, and each ball will contribute zero net work, so the entire device contributes zero net work. Depending on the exact starting state, we might be able to get a little work out of it until the next ball reached the water, but you couldn't make it run and run forever.
Note: There are more small effects we could account for, e.g. the pressure changing slightly during the process of submerging the balls, the buoyancy of the air, etc. You can add more details like this into the analysis, but the basic conclusion will remain unchanged.
The energy needed to submerge a ball is equal to the energy gain from other ball to emerge from the water on the other side, so any waste on friction drives the process impossible.
The energy needed to push a sphere into the water at the dotted line is $$E=Fs=\int PA ds=P_{water}V_{sphere}$$
I leave this incomplete because Mark Eichenlaub already answered the question. Note that since it required some energy to put the balls in the configuration shown in the questioner's diagram, essentially you'd just get that energy back by letting the water flow into the empty space and cutting the air balls so that they can float to the top. If left in its current state it should remain stationary due to force equilibrium. (no perpetual motion).
