This object is in space with it's centre of mass at point O. I can't understand how the object will react and rotate due to the force couple. In my mind i picture the object rotating around the midpoint of the two forces but can't prove it. How can i calculate the centre of rotation, how does the centre of mass react and why? ( Please keep the answer with minimal mathematics if possible )
Thanks in advance.
Net force is zero so no translational acceleration of the centre of mass.
The two forces which are acting are a couple which produces a torque independent of any reference point/axis and so there is only an angular acceleration about the centre of mass.
You may find the answers to this question, What is the proof that a force applied on a rigid body will cause it to rotate around its center of mass?, helpful?
The force diagram for this situation is shown below.
I now agree with @Farcher answer, though it was (and still is) counter-intuitive to me. I am more conversant in statics and mechanics of materials then dynamics. In statics you can move a couple and it has no effect on the requirements for static equilibrium. But in mechanics of materials, where you evaluate the magnitude and location of shear and bending stresses, you cannot move the couple. That appears not to apply in the case of dynamics of rigid bodies.
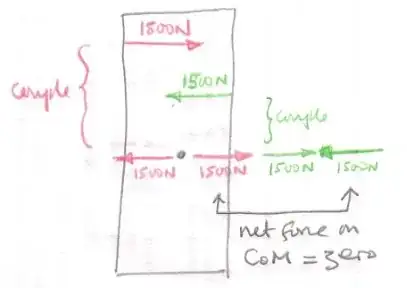
You might consider the following as a way of proving that you can move the couple anywhere on the object without changing the moment about any point on the object:
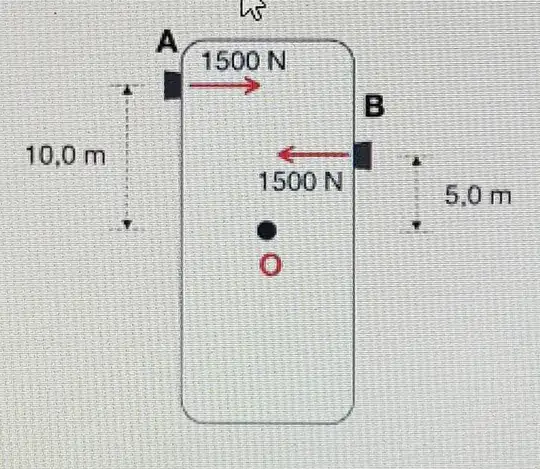
What is the sum of the moments about the point exactly in between the two forces? It is 5 x 1500 = 7500 Nm clockwise.
Now take the sum of the moments about the center of mass. It is also 5 x 1500 = 7500 Nm clockwise.
In fact, if you take the sum of the moments about ANY point on the object, you will always get 7500 Nm clockwise. This shows to me that, for dynamics, the couple can be moved anywhere.
Hope this helps.
