Why does rotation happens about hinge point in a bar when net force acting on it are zero?

Question

I have asked this question previously but not got any proper answer relevant to its free body diagram.Few are saying the body will not be in translational equilibrium as a horizontal force will appear at hinge but how that force will appear because that point is stationary.Please anyone explain i am confused?

Answer 1

Why does rotation happens about hinge point in a bar when net force acting on it are zero?

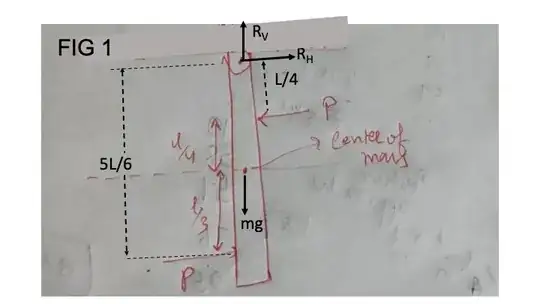
The short answer is because there is a net torque about the hinge pin caused by two equal, opposite, and parallel forces which constitute a force-couple, or simply a "couple", resulting in no net force on the bar. From the free body diagram (FBD) of FIG 1 below, the sum of the horizontal forces is

$$\sum F_{H}=R_{H}+P-P=0$$ $$R_{H}=0$$

The sum of the moments (torques) about the hinge pin, taking counter-clockwise torque as positive is

$$\sum M=\frac{5}{6}PL-\frac{1}{4}PL=\frac{7}{12}PL$$

Notice that this same torque about the hinge could be produced by a single force $P$ applied a distance $\frac{7}{12}L$ from the pin. However, in order for there to be no net horizontal force on the bar, we would then require a horizontal reaction at the hinge of $R_{H}=-P$.

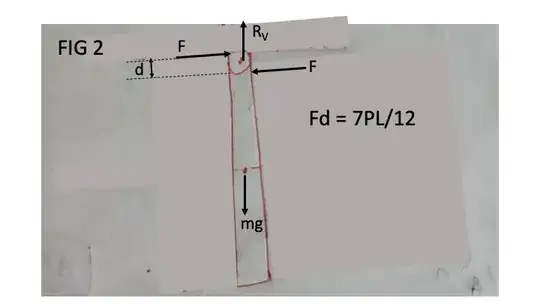
What makes a couple unique is that the moment about any point along the bar, including the COM and the hinge, is the same and equals $\frac{7}{12}PL$. For this reason a couple is called a "free vector", meaning it can be moved anywhere on the body, including the hinge, and have the same external effect on the body. See FIG 2. FIG 2 is equivalent to FIG 1 with the free moment vector moved to the hinge. To further understand why, see the accepted answer to this question: https://physics.stackexchange.com/questions/535963/force-couple-off-centre-of-mass-in-space#:~:text=2%20Answers&text=Net%20force%20is%20zero%20so,about%20the%20centre%20of%20mass.

CONCLUSION: The net torque at the hinge, assumed to be ideal (frictionless), produced by the couple (a free vector) causes the COM to rotate counter clockwise about the hinge. Because the net torque is produced by a couple, instead of a single force, there is no horizontal reaction at the hinge.

Hope this helps.

Answer 2

Why won't rotation happen? That is dependent upon torque, not force. Translational and rotational equilibrium are independent of each other. Moreover, the object is not at translational equilibrium here because of because of a hinge force, the magnitude of which you can calculate this way:

1. Find out torque about hinge.
2. Using this information, find out angular acceleration of rod.
3. Hence, Find out acceleration of CM of rod.
4. Use Newton's Second law to find out horizontal component of hinge force.

Answer 3

Assuming the two P's represent equal horizontal forces acting at equal distances from the center of mass, then the associated torques would tend to rotate the rod about the CM without moving the CM. This rotation would require the ends of the rod to move relative to the CM. But, the upper end is constrained by the axle which would have to exert a horizontal force to prevent such motion. For rotation about the axle, the two torques are not equal.

Answer 4

Imagine what would happen if the rod was not hinged, it would rotate about a the COM of rod (and not about mid point of forces (see Farcher's answer). The Hinge reaction develops to counter this rotation resulting in a net force on the COM of the rod.

The hinge reaction is the reason why the COM of the rod moves.

Answer 5

the answer is pretty simple... :)

The thing is here the rod is not an isolated system. The rod is connected to a VERY MASSIVE wall through a hinge. So the net force due to $P$ ​equals zero means that the centre of mass of the whole system... including wall and rod remains stationary, which is true...

if the rod was isolated and free, then your argument would have been correct. It would rotate about rod's COM.

Note : By considering the reaction force from the hinge, we are essentially taking the rod out from the rod+wall system. And hence, all other answers here explain the same thing

Answer 6

Here is a simple philosophy to understand the deal with forces and torques:

Action of forces of force vector at any point on a rigid body, given that it's in the same direction, causes the exact same acceleration but different torque. The idea is that the rotation experienced by the body due to the pushes and pulls you give it depends on the location of force.

For a more mathematical treatment, see Kleppner and Kolenkow.