If photons don't oscillate, how do they oscillate?

Question

The internet has told me seemingly contradictory things, and I hope you folks might help me sort it out.

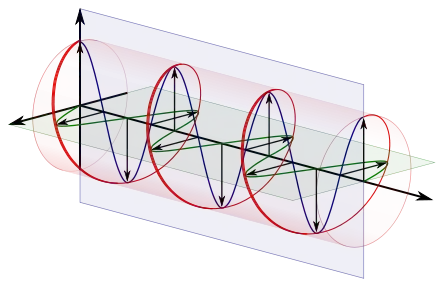
This blog post states: "Electromagnetic waves are waves from electric and magnetic fields that oscillate perpendicular to each other and to the direction of propagation." The post and this video make clear that this diagram represents an individual photon.

However, an answer on Stack Exchange states that a photon, "does not oscillate." So what is the above image of?

That answer was in a response to a question about how photons can oscillate, given that they do not experience time. It went on to explain: "it is the probability of finding [the photon] at (x,y,z,t) that has a sinusoidal distribution. Its only experiences are interactions with other elementary particles. It only has energy, momentum and spin, no oscilations describe it."

However, energy and momentum are characteristics describing a wave function, so this doesn't get away from the image of an oscilating wave. Also, I thought the wave function is the photon, which is the probability of the photon interacting (being found) somewhere. So if the wave function has a sinusoidal distribution, the photon itself has a sinusoidal distribution.

I particularly have trouble imagining how circular polarization is created by something that does not oscilate in time.

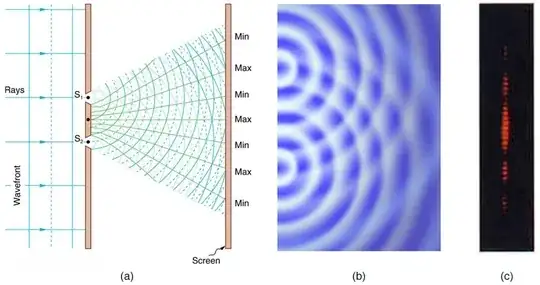
And it gets worse when I try to understand light defracting with itself.

My best guess is this: the wave function is static and unchanging, and only its position in space changes. Circular polarization happens because the position of the wave function rotates while it moves, but the wave function itself doesn't change in the process. When light defracts in the two-slit experiment, that is because the position of the photon is interfering with other parts of the same photon, but the underlying wave function remains unchanged and, in a sense, static.

Huge thanks if you can help me understand how a wave doesn't actually wave, and how or why my interpretation is off.

Answer 1

Photons are quantum objects, and it is very important that you do not think about quantum objects like classical billiard balls that have definite position or momentum. As long as the photon travels, it is delocalized. It becomes localized only when it is measured (interacted with or absorbed).

What confuses you is that you see the pictures of EM waves, including sinusodially waving trajectories, and you mistakenly (but you are not alone) think it is actually the photon itself oscillating, but what actually oscillates is the E and M field components, not the photon itself.

In light propagation, oscillation does not mean any movement in space. It is the value of the electromagnetic field, at one given point in space, that oscillates. For electromagnetic waves, there is no matter or photons that go up and down. Instead, you have to imagine that there is a little arrow associated to each point in space: this little arrow is the electric field direction. Another arrow, at the same point, is the magnetic field. These two arrows change size and direction with time, and in fact they oscillate.

How to imagine the electromagnetic waves?

The electromagnetic wave is described by the solution of classical maxwell's equation which has a sinusoidal dependence for the electric and magnetic fields perpendicular to the direction of motion of the wave. It is called a wave for this reason and the frequency is the repetition rate of the sinusoidal pattern. A single photon has only a detection probability distribution that "waves", as explained above. It is not a wave.

Can photons oscillate?

I actually asked a question about this:

Do photons oscillate or not?

Answer 2

So if the wave function has a sinusoidal distribution, the photon itself has a sinusoidal distribution.

The root to your misunderstanding lies in the above sentence. The wavefunction does not describe the photon. It is $Ψ$, a sinusoidal solution of a differential equation . Its only connection with the photon measured in lab comes through $Ψ^*Ψ$, and that is the probability of finding a given photon at an (x,y,z,t). The photon's probability of being at (x,y,z,t) has a sinusoidal distribution.

This may help you understand the difference between light and photons, the double slit experiment with single photons.

Figure 1. Single-photon camera recording of photons from a double slit illuminated by very weak laser light. Left to right: single frame, superposition of 200, 1’000, and 500’000 frames.

On the left is the footprint of single photons, their (x,y) on the screen at location (z) (time is not recorded) . They look random, but as their number builds up the classical light interference appears. That is how the point like photons of the standard model of particle physics manage to build up classical electromagnetic radiation. This can be proven mathematically too, not only experimentally.

This image may help you understand how pointlike spin 1 photonscan build up polarized light:

The photon because of its zero mass has to have its spin point either in its direction of motion, or against it.