Momentum conservation with photons

Question

Take a body having mass $M$ and velocity $v$, it has initial momentum $Mv$. The body radiates two photons of the same "mass" in directly opposite directions (one at the body motion direction, one - opposite direction). The momentum of the system gets reduced: $(M-2m)v + mc - mc = Mv - 2mv$. Does it mean, that the body velocity is increased or there is some other explanation for the missing momentum?

Answer 1

Whatever is emitting these photons is indeed faster at the end. It has to have the same momentum with less mass, and so its speed is higher after the emission.

Note that you have to be careful about what you mean by emit two photons with "the same momentum." Is this the same momentum in the original object's reference frame, or in the laboratory frame? These give quite different results.

Also note that you have some misconceptions about the relationship between mass and energy- we usually describe the photon as massless: it has energy and momentum but no mass. Rather than $E=mc^2$, a formula like $E=\sqrt{m^2c^4+p^2c^2}$ is more applicable here.

Answer 2

Check out this recent paper. It analyzes your problem (toward the bottom), using a quantized atom and field. The conclusion is: the emitter loses momentum, but this loss is not related to an acceleration. Rather, the emitter's mass changes.

In the emitter' rest frame, it cannot be accelerated because it is emitting photons of equal frequency in opposite directions. But two detectors of the photons that are moving relative to the emitter would see differently-Doppler-shifted photon frequencies, and would thus conclude that the emitter's momentum has changed. Indeed it has, but since it cannot have been accelerated, the change must come from mass.

\begin{equation} F=\frac{dp}{dt}=m\frac{dv}{dt}+\frac{dm}{dt}v \end{equation}

Answer 3

You can't use Newtonian mechanics to explain this decay because, as you pointed out, it leads to unphysical results. Using special relativity everything makes sense: the photon has a four-momentum $p^{\mu}$ where $p^0 = E = c|\vec{p}| $ and $p^i$ is the $i$-th component of the momentum (as you see I have no mass involved in these equations).

The particle before decaying in the "laboratory frame" has instead $p^0 = m \gamma c^2$ and momentum $p^i = m\gamma v_i$. If the particle has velocity along the $\hat{x}$ axis, then $p^1 = m\gamma v$ and $p^2 = p^3 = 0$.

Using the four-momentum conservation law (i.e. energy conservation + momentum conservation) you have:

$$ m \gamma c^2 = |\vec{p}|_{\gamma_1} c + |\vec{p}|_{\gamma_2} c $$ $$ m \gamma v = p^1_{\gamma_1} + p^1_{\gamma_2} $$ $$ 0 = p^2_{\gamma_1} + p^2_{\gamma_2}$$ $$ 0 = p^3_{\gamma_1} + p^3_{\gamma_2}$$

The physics you get from this is that the two photons don't have opposite momenta, neither the same energy (in the laboratory frame)! Moreover you have 6 variables but only 4 equations, which means you can't predict the direction of emission.

Answer 4

Take a body having mass M and velocity v, it has initial momentum Mv. The body radiates two photons

The pi0 for example.

of the same "mass"

the mass of photons is zero and is the same for all photons.

in directly opposite directions (one at the body motion direction, one - opposite direction).

This is wrong, unphysical.

If the photons go into opposite directions you are at the center of mass of the decaying particle by definition.This means zero initial momentum for the decaying particle.

If the decaying particle has momentum the angle between the two photons will be less than 180 degrees and they will carry the original momentum , each photon having p=E/c, i.e. the energy(frequency) of the photons is increased over the energy in the center of mass frame.

The invariant mass of the two photons ( i.e. the four vector of the addition of the two fourvectors) , will be the mass of the original particle ( the pi0 mass for example) and the system carries the original momentum.

Here is the outline of a pi0 decay in a bubble chamber (go to the index for pi0 to see the full complicated picture, and a second example)

Edit after comment that it is a solid body emitting two photons in opposite directions:

Again the mass of each photon is zero. It is the energy that describes a photon and its momentum is E/c. for two photons in equal and opposite direction of the moving body,

E1/c-E2/c will be the momentum missing from the whole body momentum.

If E1=E2 in the center of mass system of the body, no momentum is transmitted. The energy of the body in the center of mass system ( relativistically calculated) will be less than the energy E1+E2. In a moving frameof reference the momentum of the photons will be doppler shifted with respect to the one in the center of mass .

Answer 5

In my opinion, an energy-momentum diagram (the energy-momentum analogue of a spacetime diagram) can clarify what is happening. I've drawn it on rotated graph paper so that the light-signals can easily be drawn. In addition, quantitative calculations (often done with various formula from relativity) can be read off from this diagram... but I won't discuss this point now.

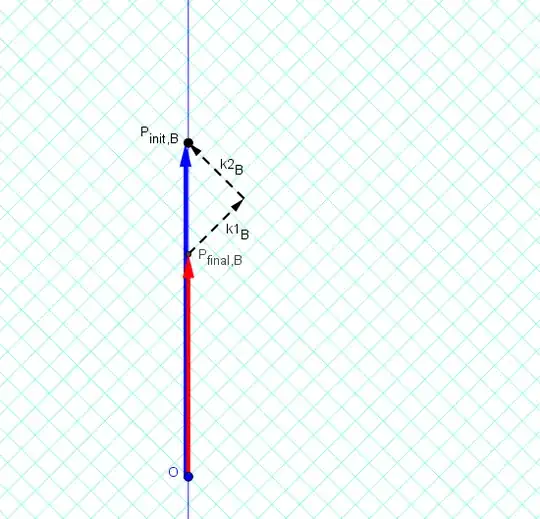
Conservation of total 4-momentum requires: $$\tilde P_{fin}+\tilde {k_1}+\tilde {k_2}=\tilde P_{init}$$

---

Here is the situation in the rest-frame of the emitter (observer B).
In this frame, the photons have the same energy and equal-magnitude but oppositely-directed spatial-momentum.

The final 4-momentum of the emitter must be smaller than the initial 4-momentum of the emitter. However, note that the emitter's 4-velocity (the "normalized 4-momentum", which is the emitter's 4-momentum divided by the emitter's rest mass) is unchanged.

---

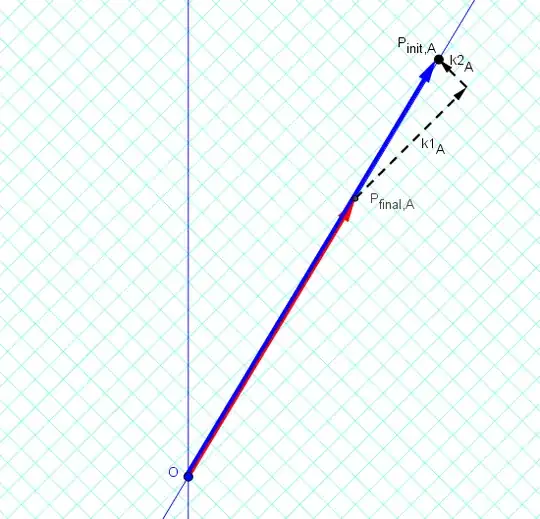
Here is the situation in the lab-frame (observer A), who observes the emitter moving with $\beta=3/5$ [from O, count 5 diamonds up and 3 diamonds to the right to see this].
In this frame, the photons have the different energy and spatial-momentum, in accordance with the Doppler Effect (with $\beta=3/5$, the Doppler factor is $k=2$).
Of course, each photon still travels at the speed of light.

The forward photon in the lab frame has
twice the 4-momentum compared to the forward photon in the emitter-frame.
The backward photon in the lab frame has
half the 4-momentum compared to the backward photon in the emitter-frame.
(Geometrically, the area of the triangle is the same in the two frames, as required by a Lorentz transformation [whose determinant equals 1].)

Once again, we see that the final 4-momentum of the emitter must be smaller than the initial 4-momentum of the emitter. And again, the emitter's 4-velocity (which is the emitter's 4-momentum divided by the emitter's rest mass) is unchanged.

In the lab frame, the emitter travels with the same spatial-velocity after emitting the photons.

As @Luc said in the Oct 12 comment, if you want to change the spatial velocity of the emitter, emit photons of different energies in the emitter-frame.

Answer 6

You seem to want that the two photons have the same energy, which I will denote by $E_\gamma$. Then the conservation of energy and momentum reads

$$\begin{align} E &= E' + 2E_\gamma\\ p &= p' \end{align}$$

where primed letters mean "after emission". With the relativistic expression of energy and momentum, these equation reads

$$\begin{align} m\gamma &= m'\gamma' + 2E_\gamma \tag{E}\\ m\gamma v &= m'\gamma'v', \tag{P} \end{align}$$

where $\gamma=(1-v^2)^{-\frac{1}{2}}$ and similarly for the primed one. Note that I am using units where the speed of light $c=1$.

Ok, after all, if I went that far, it's stupid to pretend to leave the rest as an exercise. So, divide the second equation by the first to get

$$v'=\frac{v}{1-\frac{2E_\gamma}{m\gamma}}.$$

Therefore $v'\ge v$. The equality is for the case where $v=v'=0$, i.e. when the analysis is done in the rest frame of the source emitting the two photons.

By the way, note that $m'< m$. That's because of eqn (P) since $u\mapsto (1-u^2)^{-\frac{1}{2}}u$ increases with $u$. Well, in the rest frame just mentioned, this reasoning does not hold of course, since (P) is $0=0$ but then eqn (E) becomes

$$m-m'=2E_\gamma,$$

and since $E_\gamma>0$, we still have $m>m'$.

Answer 7

By the definition of the problem, I assume by equal photon "mass" you mean equal energy. Therefore, $\lambda_L=\lambda_R=\lambda$.

The energy of a photon is $E=\frac{hc}{\lambda}$.

To see that the velocity of the object after light emission, $v_f$, increases compared to before, $v_0$, use simple Newtonian momentum analysis.

We can for back of the envelope purposes assume $E=mc^2$ applies to the photon; therefore, the mass of a photon can be assumed to be $m_\lambda=\frac{h}{\lambda c}$.

Given all of this set up the Newtonian momentum analysis as a sum of momentum before light emission equations the sum of momentum after light emission.

$m_0v_0=(m_0-2m_\lambda)v_f + m_\lambda c - m_\lambda c$

$\frac{v_f}{v_0}=\frac{m_0}{m_0 - 2\frac{h}{\lambda c}}>1$

Intuitively speaking is it that surprising that the object speeds up? Let's say you're floating in space at $5m/s$ and you throw two baseballs: one in front of you (in direction of your velocity) and one behind you. Relative to a stationary observer, they see both baseballs going $10m/s$. That means you threw one to the front $5m/s$ relative to you, and one to the rear $15m/s$ relative to you. Of course, you speed up.

In the context of relativity, another way to look at it is from the perspective of the moving object's inertial frame. If the wavelengths were equal from the original inertial frame, then they are not equal from the moving object's inertial frame (due to relativistic doppler shifting). From the perspective of the object's inertial frame, the light emitted to the rear had to have a shorter wavelength than the light emitted to the front; therefore, more momentum was ejected to the rear than the front causing the object to speed up.

Looking back at the diagram above with $v_0=0$ and $\lambda_L\ne\lambda_R$. Let $\lambda$ be the lambda measured from the original reference frame.

$\lambda_L=\lambda\sqrt{\frac{1-\frac{v}{c}}{1+\frac{v}{c}}}$

$\lambda_R=\lambda\sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$

$\therefore \lambda_L<\lambda_R$

Conducting the momentum analysis again yeilds:

$m_0v_0=(m_0-m_L-m_R)v_f - m_L c + m_R c$

$m_0(0)=\left(m_0-\frac{h}{\lambda_L c}-\frac{h}{\lambda_R c}\right)v_f - \frac{h}{\lambda_L c} c + \frac{h}{\lambda_R c} c$

$\frac{h}{\lambda_L} - \frac{h}{\lambda_R} =\left(m_0-\frac{h}{\lambda_L c}-\frac{h}{\lambda_R c}\right)v_f$

$v_f = \frac{\frac{h}{\lambda_L} - \frac{h}{\lambda_R}}{m_0-\frac{h}{\lambda_L c}-\frac{h}{\lambda_R c}}$

$\frac{h}{\lambda_L} - \frac{h}{\lambda_R}>0$

$m_0-\frac{h}{\lambda_L c}-\frac{h}{\lambda_R c}>0$

$\therefore v_f>0~\blacksquare$