The magnetic field strength, H looks very different inside a bar magnet as shown below 
I have two main questions regarding this,
why can we regard ‘magnetisation poles’ as the sources of H. When I look at the equations ($H=\frac{B_0}{\mu_0} - M$) I just can’t see where it’s coming from?
why do the field lines in the centre become more spaced (I.e. the field gets weaker) and thus isn’t uniform like B?
The two equations of Maxwell (Ampere) when specialized for static magnetic fields are $$\textrm{div}\textbf{B}=0 \\ \textbf{curl} \textbf{H}=0$$ The relationship between the two kinds of magnetic vector fields is $$\textbf{B}=\mu_0(\textbf{H}+\textbf{M}).$$ Here $\textbf{M}$ is the magnetic dipole moment density of the ponderable matter in which the two fields exist simultaneously. Of course, $\mu_0$ is just a dimensional conversion scaling factor without physical significance. In empty space (vacuum) $\textbf{M}=0$ and the two fields B and H are essentially the same just being measured in different physical units although some physicists would also argue over this.
Now consider Helmholtz's decomposition theorem, see 1, and write $\textbf{M}$ as the sum of a lamellar field and of a solenoidal field, and assume that the integration is carried over all space and that the dipole density is zero at infinity, then:
$$\textbf{M}= -\textrm{grad} \Phi + \textbf{curl}\textbf{A}$$ where the $\Phi$ is the scalar and $\textbf{A}$ is the vector potential: $$ \begin{align} \Phi(\mathbf{r}) & =\frac 1 {4\pi} \int_V \frac{\textrm{div} '\cdot\mathbf{M} (\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} \, \mathrm{d}V' \\[8pt] \mathbf{A}(\mathbf{r}) & =\frac 1 {4\pi} \int_V \frac{\textbf{curl}'\mathbf{M}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} \, \mathrm{d}V' \end{align} $$ This is an identity for any "wellbehaving" smooth vector field.
Now we identify the terms as $$\textbf{H}= \textrm{grad} \Phi \\ \textbf{B}= \mu_0\textbf{curl}\textbf{A}$$ therefore upon substitution
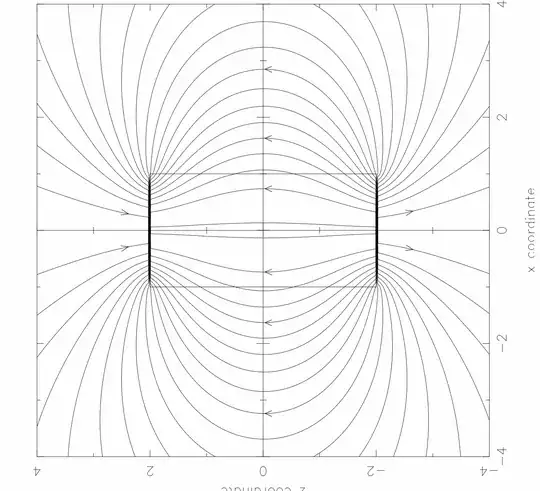
$$ \begin{align} \textbf{M}= -\frac 1 {4\pi} \textrm{grad} \int_V \frac{\textrm{div} '\mathbf{M} (\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} \, \mathrm{d}V' + \frac 1 {4\pi} \textbf{curl} \int_V \frac{\textbf{curl}'\mathbf{M}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} \, \mathrm{d}V' \end{align} $$ And here we can see explicitly that in the presence of polarized matter the source of the H-field is the divergence of M, while the source of the B-field is the curl of M.
When looking at a finite piece magnet where M discontinuously changes to zero outside the magnet neither the div nor the curl exist and the integrands get replaced by terms $$\textrm{div}'\mathbf{M}\mathrm{d}V' \rightarrow -\textbf{n}\cdot \textbf{M}' \mathrm{d}S'\\ \textbf{curl}'\mathbf{M}\mathrm{d}V' \rightarrow \textbf{n}\times \textbf{M}' \mathrm{d}S'\\ $$
The interesting term here is $\mathrm{d} q_m'=-\textbf{n}\cdot \textbf{M}' \mathrm{d}S'$ representing an infinitesimal surface charge $\mathrm{d}q_m'$ over an infinitesimal area $\mathrm{d}S'$, where $\textbf{n}$ is the outward normal of the surface of the magnetic material, and thus we have a magnetic surface charge density $\sigma'=-\textbf{n} \cdot \textbf{M}'$ caused by the discontinuity in M. Its field (the gradient term in the decomposition) of this magnetic surface charge is actually in the opposite direction of the "curl" term, so it is subtracted from it.
the things were explained in great detail in the previous answer. To be able to put it simply, one can note that the Maxwell equation in the absence of free currents is written rot (H) = 0 and div (B) = 0 which gives div (H) = -div ( M) We see that they are the same equations as those of electrostatics with a density of "magnetic charge" fictive -div (M). For uniform magnetization, -div (M) gives a surface density -M on the right and + M on the left in the figure. As a result, the field H in the figure is the same as the electrostatic field between the plates of two uniformely charged plates (wit the presence of edge effects if th plates are not infinite). If the plates are "small", the field is dipolar. Maybe it can help to understand its form without calculation. It is also understood that it is "demagnetizing" because it is directed in the opposite direction to M. (Sorry, I am new to this forum and I do not master the equation editor and English is not my native language).
