Magnetic field outside of permanent magnet - What is $\vec H$?

Question

If a cylindrical magnet has a uniform magnetization $\vec{M}$ along its axis its magnetic field $\vec{B}$ looks approximately like this:

There seems to be a contradiction to me. Since there are no free currents anywhere, $\nabla \times \vec H = \vec{0}$ everywhere. But also, $\vec{B} = \mu_0(\vec{H} + \vec{M})$ everywhere. Then, because $\vec{M} = \vec{0}$ outside of the magnet, $\vec{H}$ has to be nonzero outside of the magnet, because clearly $\vec{B}$ is not zero there. But according to the Griffith's textbook, $\vec{H}$ is the magnetic field only due to free currents, or alternatively, the field that remains if one were to remove all magnetization. So if $\vec{H}$ is nonzero outside of the magnet, and it is not caused by free currents (because there are none), and it also is not caused by the magnetization, then what is $\vec H$ and why does it exist in this case?

Answer 1

The curl of ${\bf H}$ is caused by free currents.

The H-field itself is defined as $({\bf B} - {\bf M})/\mu_0$ and since ${\bf M}=0$ outside the magnet then ${\bf H}={\bf B}/\mu_0$ and is curl-free.

Answer 2

The equations satisfied by $\vec{H}$ are : $\vec{\nabla} \times \vec{H}=\vec{0}$ and $\vec{\nabla} \cdot \vec{H} = - \vec{\nabla} \cdot \vec{M} $

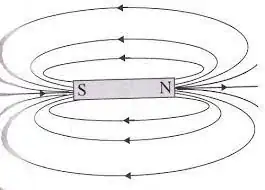
One might think that $\vec{\nabla} \cdot \vec{M} = 0$ because $\vec{M} $ is uniform. But it's wrong. We must not forget that $\vec{M} $ is discontinuous on the surface. Using the distribution's formalism, we can show that $\vec{\nabla} \cdot \vec{M} $ corresponds to two surface layers $\sigma = -M$ on the upper face and $-\sigma = + M$ on the underside (The "magnetic charges" at the poles of the magnet). Finally, the vector $\vec{H} $ has the same shape as the electrostatic field of a plane capacitor. But it is directed downwards: it is the "demagnetizing" field which tends to demagnetize an open magnet.

If the magnet is very long, we find that $\vec{H} \rightarrow \vec{0}$ except near the edges. The magnetic field $\vec{B} $ then tends towards $\mu_0 \vec{M} $ inside the magnet and towards $\vec{0} $ outside.

In electrical engineering, it is sometimes stated that the field $\vec{H}$ is controlled by free currents but this is only true if the demagnetizing field is zero. In particular, this is true for a torus or a very long cylinder. It is this type of geometry which is used to obtain the hysteresis cycle of a magnetic material and indeed, in this case, the vector $\vec{H}$ is directly controlled by the intensity which circulates in the winding of the primary. (If the secondary is traversed by a negligible current)

We could also obtain $\vec{B} $ directly by using the equivalent magnetization currents: $\vec{j_m} = \vec{\nabla} \times \vec{M}$ .

We will have : $\vec{\nabla} \times \vec{B}=\mu_0 \vec{j_m}$ and $\vec{\nabla} \cdot \vec{B} =0$

Again, one might think that $\vec{j_m} = \vec{\nabla} \times \vec{M} = \vec{0}$ But it's wrong. Again, we must not forget that $\vec{M} $ is discontinuous on the surface. Using the distribution's formalism, we can show that $\vec{j_m} = \vec{\nabla} \times \vec{M}$ corresponds to surface current $\vec{j_m} = \vec{M} \times \vec{n} = M \vec{e_\theta}$ . Clearly, the vector $\vec{B} $ has the same shape as the magnetic field of a solenoid.

One can note that with this equivalence, one proves "rigorously" that the magnetic field outside an "infinite" solenoid tends towards $0$. But it is a bit tortuous method!

Hope it can help and sorry for my poor english.