What is meant by the statement that 'The unit vectors in the cylindrical coordinate system are functions of position'. And, comparatively, how are unit vectors of rectangular coordinate system are not dependent on coordinates.
2 Answers
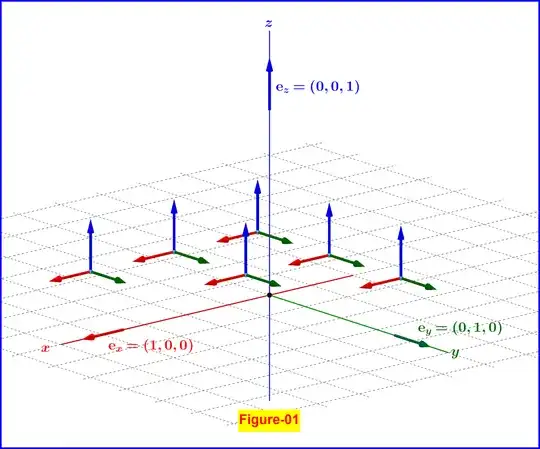
As we see in Figure-01 the unit vectors of rectangular coordinates are the same at any point, that is independent of the point coordinates.
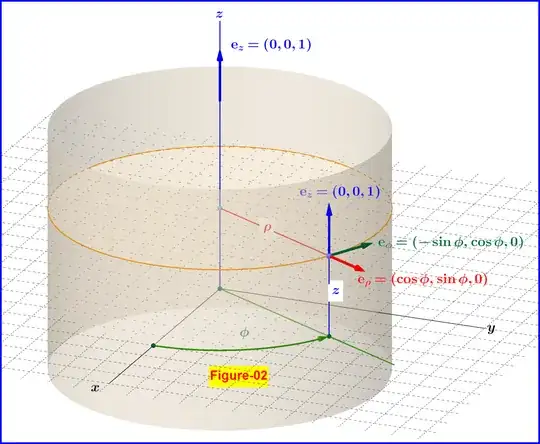
But in Figure-02 the unit vectors $\;\mathbf{e}_\rho,\mathbf{e}_\phi \; $ of cylindrical coordinates at a point depend on the point coordinates and more exactly on the angle $\;\phi$. The unit vector $\;\mathbf{e}_z\;$ is independent of the cylindrical coordinates of the point.
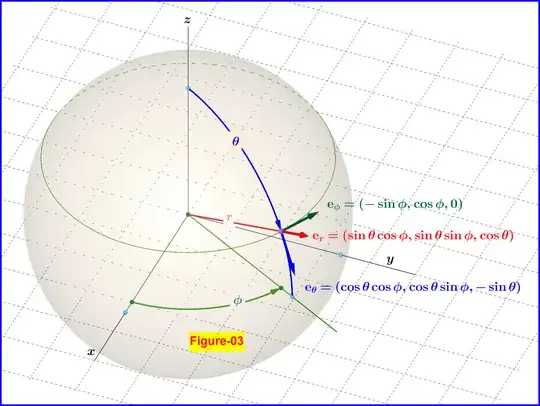
In spherical coordinates, Figure-03, the unit vectors depend on the azimuthal and polar angles $\;\phi\;$ and $\;\theta\;$ respectively.
- 16,825
- 2
- 45
- 73
Even though this is more of a math problem, I figured typing up an answer is less trouble than trying to migrate the question. And many physics problems depend on our understanding of coordinate systems.
Let's think about polar coordinates in the x-y plane, since cylindrical coordinates is just this with an added z-coordinate.
Let's say we are on the unit circle ($r=1$). Now, when $\theta=0$, the radial unit vector points along the positive x-axis. But what if $\theta=\pi$? Then the radial unit vector points along the negative x-axis. You can pick any other angle and see the radial unit vector points along a different direction. Same for the $\theta$ unit vector.
Now what about our Cartesian unit vectors? Well these are always parallel to their respective axes, and these axes are fixed. Therefore, these unit vectors do not depend on location.
- 59,060