What equation of state is needed for liquid states?

Question

I'm familiar with the ideal gas law $$PV=nRT$$ but I don't think it applies to liquids like water. If I'm wrong, please correct me! If I'm right, then what equation of state applies to liquids such as water?

Answer 1

Supercritical fluids are well described by real and ideal gas laws.

A common equation of state for both liquids and solids is

$$V_m = C_1 + C_2 T + C_3 T^2 - C_4 p - C_5 p T$$

where $V_m$ is molar volume, $T$ is temperature, $p$ is pressure, and $C_1$, $C_2$, $C_3$, $C_4$, and $C_5$ are empirical constants, all positive and specific to each substance.

The Peng & Robinson equation of state has been found to be useful for both liquids and real gasses:

$$p = \frac{RT}{V_m - b} - \frac{a(T)}{V_m (V_m + b) + b (V_m - b)}$$

where $a$ and $b$ are empirical constants and $R$ the ideal gas constant.

Answer 2

For all intents and purposes, you can use an incompressible equation of state:

$$ V = constant $$

That's it. No matter what pressure and temperature, you have the same volume. It's not completely true, but in relation to gasses it is true enough to make it that pressure work is negligible in liquids compared to gasses, and for liquids, you can just deal with the heat content without considering any work done in the expansions and contractions required to change temperature.

Answer 3

Accurate equations of states (EOS) for real gases, liquids, or solids are (in contrast to nice theoretical models such as an ideal gas or debye solid) quite complex, and must be fitted to experimental data.

For example, a very accurate equation of state for water and steam can be found in
Wagner and Pruss, The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, 1995
http://www.teos-10.org/pubs/Wagner_and_Pruss_2002.pdf

But the water EOS is not very intelligible, except for a computer.

Answer 4

To add just a bit to Ron Maimon's answer, the fact is that we do not have anything like a general equation of state for liquids. They are simply too complex for present day techniques.

We can do a bit better for solids since solids have an idealized crystalline form. But even there solids are very complex.

But don't fret. The situation isn't too much better for real gases, especially around the critical point.

Answer 5

There is one you can derive for pressure and for density.

Start with:

$$\chi_T=\frac{1}{\rho}\left(\frac{\partial\rho}{\partial P}\right)_T$$

Thus by integration between $\rho_0$ and $\rho$ in one side and by $P_0$ and $P$ in the other side you'll get $$\rho=\rho_0 \exp\left(\chi_T\left(P-P_0\right)\right)$$

On a liquid column you can use it in: $$\frac{dP}{dz}=-\rho g$$

To get: $$P=P_0 - \frac{1}{\chi_T}\ln\left(1-\chi_T\rho_0g\Delta z\right)$$

Under many circumstances though, this boils down to: $$P=P_0 + \rho_0 g \Delta z$$

Because $\chi_T$ is small enough to make $\rho_0 g \Delta z$ neglectable. For instance, for water between $0 °C$ and $30 °C$, $\chi_T \approx 10^{-10}$ and even in Mariana Trench $\rho_0 g \Delta z \approx 10^3\cdot 10 \cdot 11 \cdot 10^3 \approx 10^8$ and $\ln(1-x) \approx x$ for small values of $x$ and you get the previous result. So for liquid water even in those conditions, up to $1100$ bar, you can just use the basic formula we all learn in high-school. How cool! :)

Answer 6

I would propose to use Van der Waals equation, since it's most principle one which assumes finite particle sizes, declared as

$$\tag 1 \left(p+{\frac {a}{v^{2}}}\right)(v-b)=RT,$$

where $v$ is volume per one mole of material, $b$- minimum possible specific molar volume $v$ (close packing).

Expanding LHS of (1) in Taylor series about a point $v=b$, gives :

$$ \tag 2 (v - b) \left(\frac {a}{b^2} + p\right) - \frac{2 a (v - b)^2}{b^3} + \frac{3 a (v - b)^3}{b^4} - \frac{4 a (v - b)^4}{b^5} + \frac{5 a (v - b)^5}{b^6} + \ldots $$

Now taking first term of (2) series, equating it to the $RT$ and solving relation for a specific volume $v$, gives

$$ \tag 3 v(p) = \frac{b (a + b (b p + RT))}{a + b^2 p} $$

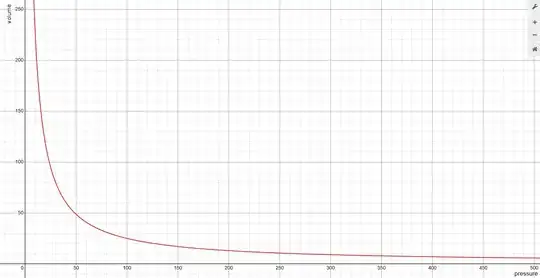
Now let's draw $v(p)$ expression, at the room temperature, for simplicity assuming $a=1,b=1$ (with their respective units for sure). What we get is this:

So by applying pressure to the liquid,- it's volume VERY fast, i.e. exponentially drops to some values near $b$, and then- whatever pressure you manage to apply to it- it will just approach $b$ asymptotically and monotonically. That's why liquids are called "incompressible",- for the most pressure scale- they are already at a close packing configuration and so you can't squeeze it no more, since liquid molecules are modelled as a bunch of hard spheres, which you can't overlay one into the other.