4

Assume we have a balloon in a tank filled with a liquid , without any gravitational forces: We just know the Temperature, $V_0$ and $V_1$

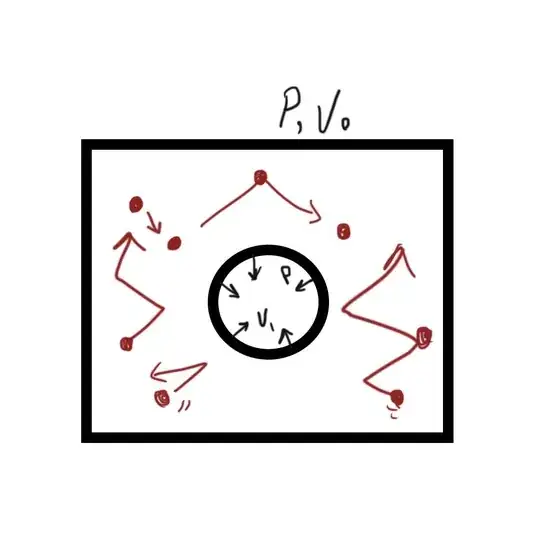
enter image description here

I want to calculate the pressure exerted from the liquid on the balloon. If it was just filled with gas I could easily calculate with $PV=nRT$, but this does not work for fluids.

Also by exclusion of gravity, the only source of pressure will be from the thermal energy ( fluid molecules moving and hitting on the balloon ) + internal cohesive energy.

UPDATE:

I think the only problem here is just finding the pressure exerted on the balloon by the liquid cohesive pressure ( in fact it is kind of equation of state problem ). I studied a lot since I asked this question. There are 2 pressures that I consider for using as P in this question:

1- Cohesive Energy density = 2.2973 GPa for water

2-Internal Cohesive Pressure= 168 MPa

My question is which one should be used here as $P$ ?

Prof Shonku
  • 687
Aug
  • 331

2 Answers2

1

Considering your comment "Actually it is just an air cavity made inside the water with no boundary material":

$P_{in} = P_{out} + 2\gamma /R$

where $R$ is the radius of the air cavity and $\gamma$ is the surface tension of the air-water interface, which is 0.072 N/m at 298K.

See Internation Tables of the Surface Tension of Water for values at other temperatures.

To calculate $P_{out}$ as a function of T and V, you need an equation of state for liquid water.

See A new analytic equation of state for liquid water J. Chem. Phys., Vol. 110, pages 484-496.

DavePhD
  • 16,314
1

You say you know the temperature and the volume of the water. Assuming that you also know the mass of the water, you know both temperature and specific volume (the inverse of the the density). You just need a thermodynamic table for the properties of liquid water like this one from NIST to find the pressure. If you actually don't have enough information to find the mass of the water, then you don't have enough information to find the pressure.

Compressed Liquid tables are normally indexed by $P$ then by $T$- i.e., there are sub-tables for different $P$ values and each sub-table is indexed by $T$. The first italicized row in the linked table tells you that if you had $T=0$ $^\circ$C then $\rho=999.8$ kg/m3 would indicate $P = 0.01$ MPa (from the 2nd column, which is in the 0.01 MPa sub-table) or $0.02$ MPa (from the seventh column).

user1476176
  • 1,511