9

The one-loop self-energy of the photon,

,

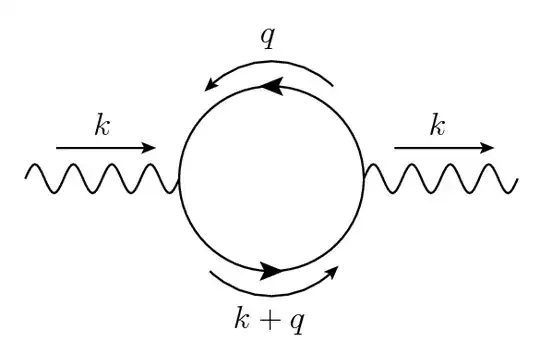when contracted with the external momentum $k^\mu$ gives the following difference of integrals where the integration variable in the first term is shifted compared to the second term.

$$ k_\mu\Pi^{\mu\nu}(k) \sim \int\frac{d^4q}{(2\pi)^4}\ \left\{ \frac{(q + k)^\nu}{(q+k)^2-m^2} - \frac{q^\nu}{q^2-m^2} \right\} .$$

The argument for this result to be zero is based on the fact that a constant shift in the integration variable does not change the integral, which claim is in fact contingent on the assumption that the integral is convergent or at most logarithmically divergent.

In our case, the integrals are cubically divergent, which is bad. In fact, if you follow the calculations in Schwartz Ch.30 p.625, you will find that the above difference is quadratically divergent. With a cutoff $\Lambda$, we find that

$$ k_\mu\Pi^{\mu\nu}(k) \sim \lim_{\Lambda \to \infty} \frac{ik^\nu}8 \Lambda^2 + \cdots \,.$$

Why do we then claim that the Ward identity is satisfied?

Qmechanic
  • 220,844
Nanashi No Gombe
  • 2,666

1 Answers1

3

There is no contradiction. When we calculate the photon self-energy, we always work in a regularization scheme, such as Pauli-Villars or dimensional regularization, where the integrals are perfectly finite. Then it is of course valid to shift the integration variable.

Schwartz later says shifts aren't always valid, but the context is different. In chapter 30, Schwartz is computing a correlator involving chiral fermions, where the usual regularization methods don't work: Pauli-Villars breaks chiral symmetry, and dimensional regularization can't handle $\gamma_5$. So instead Schwartz applies no regularization at all and shifts the integration variable "by hand". Since the integrals now really are divergent, this has a nontrivial effect.

knzhou
  • 107,105