Hint : We have here 3 frames and 2 Lorentz Transformations. (1) Frame $\:\mathrm S\left(x,y,z\right)\:$ (2) frame $\:\mathrm S'\left(x',y',z'\right)\:$ moving with respect to $\:\mathrm S\left(x,y,z\right)\:$ with velocity $\:\mathbf{v}=\left(v,0,0\right)\:$ along the common $\:x-,x'-$axis (3) frame $\:\mathrm S''\left(x'',y'',z''\right)\:$, the rest frame of the rod, moving with respect to $\:\mathrm S'\left(x',y',z'\right)\:$ with velocity $\:\mathbf{u}=\left(0,u,0\right)\:$ along the common $\:y'-,y''-$axis.
I suggest to take a look in my answer therein : General matrix Lorentz transformation
EDIT
We have here two 2+1-Lorentz transformations. So the axes $\:z,z',z''\:$ are ignored.
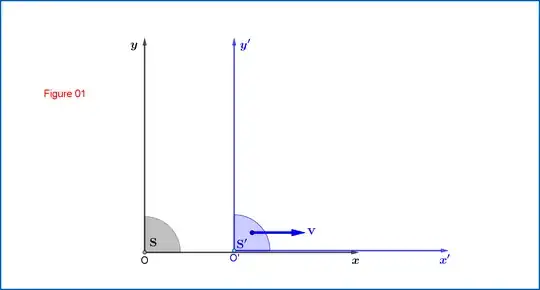
From Figure 01 :
Lorentz Transformation from $\:\mathrm{S}\equiv \{xy\eta, \eta=ct\}\:$ to $\:\mathrm{S'}\equiv \{x'y'\eta', \eta'=ct'\}\:$
\begin{equation}
\begin{bmatrix}
x'\\
y'\\
\eta'
\end{bmatrix}
=
\begin{bmatrix}
\hphantom{-}\cosh\zeta & 0 & \boldsymbol{-}\sinh\zeta \\
0 & 1 & 0 \\
\boldsymbol{-}\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
\eta
\end{bmatrix}
\,, \quad \tanh\zeta=\dfrac{v}{c}
\tag{01}
\end{equation}
or
\begin{equation}
\mathbf{X'}=\mathrm{L'}\mathbf{X}\,, \qquad \mathrm{L'}=
\begin{bmatrix}
\hphantom{-}\cosh\zeta & 0 & \boldsymbol{-}\sinh\zeta \\
0 & 1 & 0 \\
\boldsymbol{-}\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\
\end{bmatrix}
\tag{01"}
\end{equation}
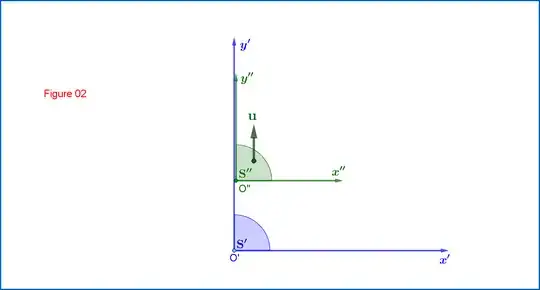
From Figure 02:
Lorentz Transformation from $\:\mathrm{S'}\equiv \{x'y'\eta', \eta'=ct'\}\:$ to $\:\mathrm{S''}\equiv \{x''y''\eta'', \eta''=ct''\}\:$
\begin{equation}
\begin{bmatrix}
x''\\
y''\\
\eta''
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 \\
0 &\hphantom{-}\cosh\xi & \boldsymbol{-}\sinh\xi \\
0 & \boldsymbol{-}\sinh\xi & \hphantom{-}\cosh\xi \\
\end{bmatrix}
\begin{bmatrix}
x'\\
y'\\
\eta'
\end{bmatrix}
\,, \quad \tanh\xi=\dfrac{u}{c}
\tag{02}
\end{equation}
or
\begin{equation}
\mathbf{X''}=\mathrm{L''}\mathbf{X'}\,, \qquad \mathrm{L''}=
\begin{bmatrix}
1 & 0 & 0 \\
0 &\hphantom{-}\cosh\xi & \boldsymbol{-}\sinh\xi \\
0 & \boldsymbol{-}\sinh\xi & \hphantom{-}\cosh\xi \\
\end{bmatrix}
\tag{02"}
\end{equation}
Note that because of the Standard Configurations the matrices $\:\mathrm{L'}, \mathrm{L''}\:$ are real symmetric.
From equations (01) and (02) we have
\begin{equation} \mathbf{X''}=\mathrm{L''}\mathbf{X'}=\mathrm{L''}\mathrm{L'}\mathbf{X}\Longrightarrow \mathbf{X''}=\Lambda\mathbf{X}
\tag{03}
\end{equation}
where $\:\Lambda\:$ the composition of the two Lorentz Transformations $\:\mathrm{L'}, \mathrm{L''}\:$
\begin{equation}
\Lambda=\mathrm{L''}\mathrm{L'}=
\begin{bmatrix}
1 & 0 & 0 \\
0 &\hphantom{-}\cosh\xi & \boldsymbol{-}\sinh\xi \\
0 & \boldsymbol{-}\sinh\xi & \hphantom{-}\cosh\xi \\
\end{bmatrix}
\begin{bmatrix}
\hphantom{-}\cosh\zeta & 0 & \boldsymbol{-}\sinh\zeta \\
0 & 1 & 0 \\
\boldsymbol{-}\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\
\end{bmatrix}
\tag{04}
\end{equation}
that is
\begin{equation}
\Lambda=
\begin{bmatrix}
\hphantom{-}\cosh\zeta & 0 & \boldsymbol{-}\sinh\zeta \\
\hphantom{-}\sinh\zeta\sinh\xi &\hphantom{-}\cosh\xi & \boldsymbol{-}\cosh\zeta\sinh\xi \\
\boldsymbol{-}\sinh\zeta\cosh\xi & \boldsymbol{-}\sinh\xi & \hphantom{-}\cosh\zeta\cosh\xi \\
\end{bmatrix}
\tag{04"}
\end{equation}
In the following it's necessary to have the inverse transformation $\:\Lambda^{\boldsymbol{-}1}\:$ which could be determined from :
\begin{equation}
\Lambda^{\boldsymbol{-}1}=\mathrm{L\!'}^{\boldsymbol{-}1}\mathrm{L\!''}^{\boldsymbol{-}1}
\tag{05}
\end{equation}
For the inverse transformations $\:\mathrm{L\!'}^{\boldsymbol{-}1},\mathrm{L\!''}^{\boldsymbol{-}1}\:$ we have respectively
\begin{equation}
\mathrm{L'}\left(\zeta\right)=
\begin{bmatrix}
\hphantom{-}\cosh\zeta & 0 & \boldsymbol{-}\sinh\zeta \\
0 & 1 & 0 \\
\boldsymbol{-}\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\
\end{bmatrix}
\Longrightarrow
\mathrm{L\!'}^{\boldsymbol{-}1}=\mathrm{L'}\left(\boldsymbol{-}\zeta\right)=
\begin{bmatrix}
\cosh\zeta & 0 & \sinh\zeta \\
0 & 1 & 0 \\
\sinh\zeta & 0 & \cosh\zeta \\
\end{bmatrix}
\tag{06}
\end{equation}
\begin{equation}
\mathrm{L''}\left(\xi\right)=
\begin{bmatrix}
1 & 0 & 0 \\
0 &\hphantom{-}\cosh\xi & \boldsymbol{-}\sinh\xi \\
0 & \boldsymbol{-}\sinh\xi & \hphantom{-}\cosh\xi \\
\end{bmatrix}
\Longrightarrow
\mathrm{L\!''}^{\boldsymbol{-}1}=\mathrm{L''}\left(\boldsymbol{-}\xi\right)=
\begin{bmatrix}
1 & 0 & 0 \\
0 &\cosh\xi & \sinh\xi \\
0 & \sinh\xi & \cosh\xi \\
\end{bmatrix}
\tag{07}
\end{equation}
so
\begin{equation}
\!\!\!\!\!\!
\Lambda^{\boldsymbol{-}1} \!=\!
\begin{bmatrix}
\cosh\zeta & 0 & \sinh\zeta \\
0 & 1 & 0 \\
\sinh\zeta & 0 & \cosh\zeta \\
\end{bmatrix}
\!\!\!
\begin{bmatrix}
1 & 0 & 0 \\
0 &\cosh\xi & \sinh\xi \\
0 & \sinh\xi & \cosh\xi \\
\end{bmatrix}
\!=\!
\begin{bmatrix}
\cosh\zeta & \sinh\zeta\sinh\xi & \sinh\zeta\cosh\xi \\
0 &\hphantom{-}\cosh\xi & \sinh\xi \\
\sinh\zeta & \cosh\zeta\sinh\xi & \cosh\zeta\cosh\xi \\
\end{bmatrix}\!\!\!\!
\tag{08}
\end{equation}
We need also the velocity vector, let $\:\mathbf{w}$, of the translational motion of the frame $\:\mathrm S''\left(x'',y''\right)\:$ with respect to the frame $\:\mathrm S\left(x,y\right)$. This vector is the relativistic sum of two orthogonal velocity vectors $\:\mathbf{v}=\left(\upsilon\,,0\right),\mathbf{u}=\left(0\,,u\right)$(1)
\begin{equation}
\mathbf{w}=\mathbf{v}+\dfrac{\mathbf{u}}{\gamma_{\upsilon}}=\left[\upsilon\,,\left(\!1\!-\!\frac{\upsilon^{2}}{c^{2}}\right)^{\!\!\frac12}\!\!u\right]\,,\quad \gamma_{\upsilon} = \left(\!1\!-\!\frac{\upsilon^{2}}{c^{2}}\right)^{\!\!\boldsymbol{-}\frac12}=\cosh\zeta
\tag{09}
\end{equation}
not to be confused with the relativistic sum of two collinear velocity vectors pointing to the same direction
\begin{equation}
w \ne \dfrac{\upsilon\!+\!u}{1+\dfrac{\upsilon u}{c^{2}}}
\tag{10}
\end{equation}
From (09) we have
\begin{align}
\dfrac{w_{x}}{c} & = \dfrac{\upsilon}{\:\:c\:\:}=\tanh\zeta
\tag{11.1}\\
\dfrac{w_{y}}{c} & = \dfrac{u}{\gamma_{\upsilon}c}= \dfrac{\tanh\xi}{\cosh\zeta}
\tag{11.2}\\
\left(\dfrac{w}{c}\right)^{2} & = \left(\dfrac{w_{x}}{c}\right)^{2}+\left(\dfrac{w_{y}}{c}\right)^{2}=1-\left(\dfrac{1}{\cosh\zeta\cosh\xi}\right)^{2}=\dfrac{\gamma^{2}_{w}\!-\!1}{\gamma^{2}_{w}}
\tag{11.3}\\
\gamma_{w} & = \left(\!1\!-\!\frac{w^{2}}{c^{2}}\right)^{\boldsymbol{-}\frac12}=\cosh\zeta\cosh\xi=\gamma_{\upsilon}\gamma_{u}
\tag{11.4}
\end{align}
Now, let a rod of length $\:\boldsymbol{\ell}\:$ at rest in frame $\:\mathrm S''\:$ parallel to the $\:x''\!\!-$axis, see Figure 03. The end points of the rod are observed in $\:\mathrm S''\:$ simultaneously at a given time moment $\:t''\!\!-$ so we have two events $\:\mathrm 1''\:$ and $\:\mathrm 2''\:$ separated by the space-time vector
\begin{equation}
\Delta\mathbf{X''}=
\begin{bmatrix}
\Delta x''\\
\Delta y''\\
\Delta \eta''
\end{bmatrix}
=
\begin{bmatrix}
x''_{2}-x''_{1}\\
y''_{2}-y''_{1}\\
c\left(t''_{2}-t''_{1}\right)
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{\ell}\\
0\\
0
\end{bmatrix}
\tag{12}
\end{equation}
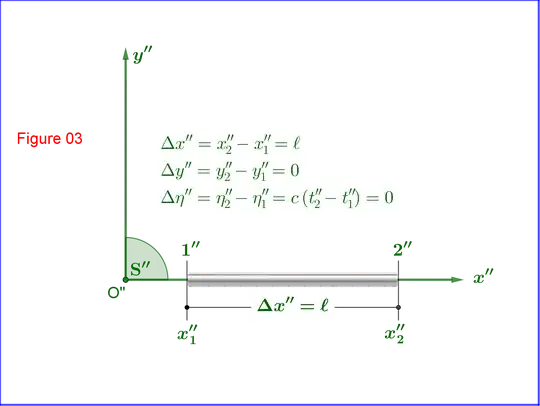
In frame $\:\mathrm S\:$ the two events are observed as two events $\:\mathrm 1\:$ and $\:\mathrm 2\:$ separated by the space-time vector
\begin{equation}
\Delta\mathbf{X}=
\begin{bmatrix}
\Delta x\\
\Delta y\\
\Delta \eta
\end{bmatrix}
=
\begin{bmatrix}
x_{2}-x_{1}\\
y_{2}-y_{1}\\
c\left(t_{2}-t_{1}\right)
\end{bmatrix}
\tag{13}
\end{equation}
which is connected with $\:\Delta\mathbf{X''}\:$ by the $\:\Lambda^{\boldsymbol{-}1}\:$ transformation
\begin{equation}
\Delta\mathbf{X}=\Lambda^{\boldsymbol{-}1}\Delta\mathbf{X''}
\tag{14}
\end{equation}
From equations (08) and (12) we have
\begin{equation}
\begin{bmatrix}
\Delta x\\
\Delta y\\
\Delta \eta
\end{bmatrix}
=
\begin{bmatrix}
\cosh\zeta & \sinh\zeta\sinh\xi & \sinh\zeta\cosh\xi \\
0 &\hphantom{-}\cosh\xi & \sinh\xi \\
\sinh\zeta & \cosh\zeta\sinh\xi & \cosh\zeta\cosh\xi
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{\ell}\\
0\\
0
\end{bmatrix}
\tag{15}
\end{equation}
so
\begin{equation}
\Delta x=\boldsymbol{\ell} \cosh\zeta \,, \quad \Delta y=0\,, \quad \Delta \eta= c\Delta t=\boldsymbol{\ell}\sinh\zeta
\tag{16}
\end{equation}
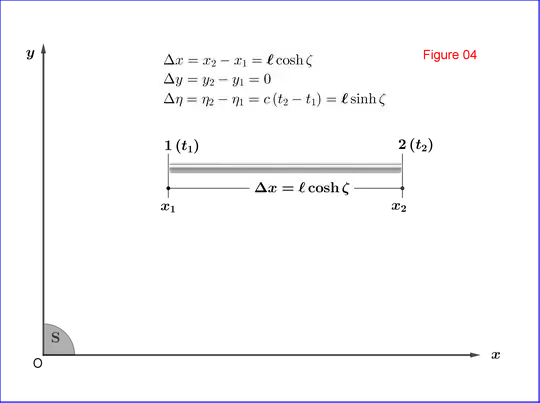
Equation (16) is represented in Figure 04. But this view is not a snapshot of the rod at a given time moment $\:t\:$ in $\:\mathrm S\left(x,y\right)$. To the contrary, it's a montage of snapshots of the points along the rod, each point shown at its own time moment. So, the end $\:\mathrm 1\:$ of the rod is shown on its position at the time moment $\:t_{1}\:$, the end $\:\mathrm 2\:$ of the rod is shown on its position at the time moment $\:t_{2}\:$ and an intermediate point $\:\mathrm 3\:$ with coordinate $\:x_{3}\in \left[x_{1},x_{2}\right]\:$ at the time moment $\:t_{3}\:$
\begin{equation}
t_{3}=t_{1}+\dfrac{x_{3}-x_{1}}{x_{2}-x_{1}}\left(t_{2}-t_{1}\right)
\tag{17}
\end{equation}
To observe the rod at a given time moment $\:t\:$ in $\:\mathrm S\left(x,y\right)$, for example at $\:t_{1}\:$, we must return the end point $\:\mathrm 2\:$ from its position at time $\:t_{2}\:$ to its position at time $\:t_{1}\:$ since $\:\mathrm 1\:$ is already shown at time $\:t_{1}$.
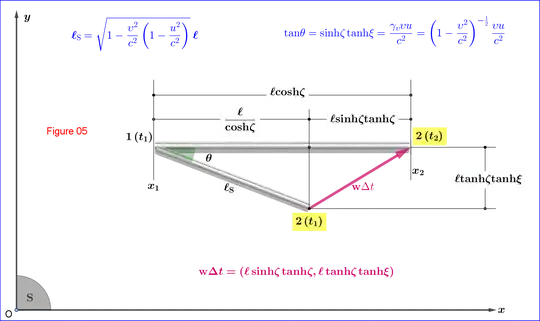
This is done in Figure 05. Since the rod is in translational motion with velocity vector $\:\mathbf{w}\:$ in frame $\:\mathrm S\left(x,y\right)$, the two positions of $\:\mathrm 2\:$ at time moments $\:t_{1},t_{2}$ are separated by the vector $\:\mathbf{w}\left(t_{2}-t_{1}\right)$ and from equations (11.1),(11.2),(16) we have
\begin{equation}
\mathbf{w}\Delta t=\!\dfrac{\mathbf{w}}{c}\Delta \eta\!=\left(\dfrac{w_{x}}{c},\dfrac{w_{y}}{c}\right)\boldsymbol{\ell}\sinh\!\zeta= \left(\tanh\!\zeta,\dfrac{ \tanh\!\xi}{\cosh\!\zeta}\right)\boldsymbol{\ell}\sinh\!\zeta
\tag{18}
\end{equation}
so
\begin{equation}
\mathbf{w}\Delta t= \left(\boldsymbol{\ell}\sinh\!\zeta\tanh\!\zeta,\boldsymbol{\ell}\tanh\!\zeta\tanh\!\xi\right)
\tag{19}
\end{equation}
From details in Figure 05 about the lengths of line segments
\begin{equation}
\tan\!\theta=\dfrac{\boldsymbol{\ell}\!\tanh\!\zeta\!\tanh\!\xi}{\dfrac{\boldsymbol{\ell}}{\cosh\!\zeta}}=\sinh\!\zeta\tanh\!\xi
\tag{20}
\end{equation}
but
\begin{equation}
\sinh\!\zeta=\underbrace{\cosh\!\zeta}_{\gamma_{\upsilon}}\underbrace{\tanh\!\zeta}_{\upsilon/c}=\dfrac{\gamma_{\upsilon}\upsilon}{c}\,, \quad \tanh\!\xi=\dfrac{u}{c}
\tag{21}
\end{equation}
so
\begin{equation}
\boxed{\:\tan\!\theta=\dfrac{\gamma_{\upsilon}\upsilon u}{c^{2}}=\left(1-\dfrac{\upsilon^{2}}{c^{2}}\right)^{\boldsymbol{-}\frac12}\dfrac{\upsilon u}{c^{2}}\:}
\tag{22}
\end{equation}
For the length $\:\boldsymbol{\ell}_{\mathrm S}\:$ of the inclined rod in frame $\: \mathrm S\:$ we have from the orthogonal triangle in Figure 05
\begin{equation}
\boldsymbol{\ell}_{\mathrm S}^{2}=\left(\dfrac{\boldsymbol{\ell}}{\cosh\!\zeta}\right)^{\!\!2}+\left(\boldsymbol{\ell}\!\tanh\!\zeta\!\tanh\!\xi\vphantom{\dfrac12}\right)^{\!\!2}=\left[1 -\dfrac{\upsilon^{2}}{c^{2}}\left(1-\dfrac{u^{2}}{c^{2}}\right)\right]\boldsymbol{\ell}^{2}
\tag{23}
\end{equation}
so
\begin{equation}
\boxed{\:\boldsymbol{\ell}_{\mathrm S}=\sqrt{1 -\dfrac{\upsilon^{2}}{c^{2}}\left(1-\dfrac{u^{2}}{c^{2}}\right)}\:\boldsymbol{\ell}\:}
\tag{24}
\end{equation}
From (22) and (24) we have verifications of the following two special cases :
If $\:\color{blue}{u=0}\:$ then $\:\theta\!=\! 0\:$, the rod is moving parallel to the $\:x-$axis with speed $\:\upsilon\:$ , contracted from $\:\boldsymbol{\ell}\:$ to $\:\boldsymbol{\ell}/\cosh\!\zeta$.
If $\:\color{blue}{\upsilon\!=\! 0}\:$ then $\:\theta\!=\! 0\:$, the rod is parallel to the $\:x-$axis with unchanged length $\:\boldsymbol{\ell}$ moving in the direction of the $\:y-$axis with speed $\:u$.
Numerical Examples :
\begin{equation}
\begin{Bmatrix}
\upsilon/c=0.60\\
u/c=0.40
\end{Bmatrix}
\quad =\!=\!=\!=\!\Longrightarrow\quad
\begin{Bmatrix}
\tan\!\theta=0.30 \\
\theta=16.70^{\,\rm o} \\
\boldsymbol{\ell}_{\mathrm S}=0.835\, \boldsymbol{\ell}
\end{Bmatrix}
\tag{25}
\end{equation}
\begin{equation}
\begin{Bmatrix}
\upsilon/c=0.80\\
u/c=0.60
\end{Bmatrix}
\quad =\!=\!=\!=\!\Longrightarrow\quad
\begin{Bmatrix}
\tan\!\theta=0.80 \\
\theta=38.66^{\,\rm o} \\
\boldsymbol{\ell}_{\mathrm S}=0.768\, \boldsymbol{\ell}
\end{Bmatrix}
\tag{26}
\end{equation}
\begin{equation}
\begin{Bmatrix}
\upsilon/c\:\longrightarrow\:1\\
u/c\:\longrightarrow\:1
\end{Bmatrix}
\quad =\!=\!=\!=\!\Longrightarrow\quad
\begin{Bmatrix}
\tan\!\theta\:\longrightarrow\:+\infty \\
\hphantom{\:\tan\theta}\theta\:\longrightarrow\:90.00^{\,\rm o} \\
\boldsymbol{\ell}_{\mathrm S}\:\longrightarrow\:\boldsymbol{\ell}
\end{Bmatrix}
\text{!!!!!!}
\tag{27}
\end{equation}
(1)
We can derive equations (11.1),(11.2) for the components of the velocity vector $\:\mathbf{w}\:$ using the Lorentz transformation $\:\mathrm{L\!'}^{\boldsymbol{-}1}\:$ between frames $\:\mathrm S',\mathrm S\:$ instead of equation (09)(the last is given without proof and comes from on a general 3+1-Lorentz Transformation)
So, suppose that the origin $\:\mathrm O''\:$ of frame $\:\mathrm S''\:$ is a particle moving in frame $\:\mathrm S'\:$ with velocity vector
\begin{equation}
\mathbf{u}=\left(\dfrac{\mathrm d x'}{\mathrm d t'},\dfrac{\mathrm d y'}{\mathrm d t'}\right)=\left(0,u\right)
\tag{ft-01}
\end{equation}
From equation (06) for the Lorentz transformation $\:\mathrm{L\!'}^{\boldsymbol{-}1}\:$ \begin{equation}
\begin{bmatrix}
\mathrm d x\\
\mathrm d y\\
\mathrm d\eta
\end{bmatrix}
=
\begin{bmatrix}
\cosh\zeta & 0 & \sinh\zeta \\
0 & 1 & 0 \\
\sinh\zeta & 0 & \cosh\zeta \\
\end{bmatrix}
\begin{bmatrix}
\mathrm d x'\\
\mathrm d y'\\
\mathrm d\eta'
\end{bmatrix}
\tag{ft-02}
\end{equation}
\begin{align}
\mathrm dx & =\cosh\!\zeta \,\mathrm d x'+\sinh\!\zeta \,\mathrm d\eta'
\tag{ft-03a}\\
\mathrm dy & =\mathrm dy'
\tag{ft-03b}\\
\mathrm d\eta & = \sinh\!\zeta \,\mathrm dx'+\cosh\!\zeta \,\mathrm d\eta'
\tag{ft-03c}
\end{align}
dividing (ft-03a) and (ft-03b) by (ft-03c)
\begin{align}
\dfrac{\mathrm dx}{\mathrm d\eta} & =\dfrac{\cosh\!\zeta \,\mathrm d x'+\sinh\!\zeta \,\mathrm d\eta'}{\sinh\!\zeta \,\mathrm dx'+\cosh\!\zeta \,\mathrm d\eta'}=\dfrac{\cosh\!\zeta \, \left(\dfrac{\mathrm dx'}{\mathrm d\eta'}\right)+\sinh\!\zeta}{\sinh\!\zeta \, \left(\dfrac{\mathrm dx'}{\mathrm d\eta'}\right)+\cosh\!\zeta}
\tag{ft-04a}\\
\dfrac{\mathrm dy}{\mathrm d\eta} & =\dfrac{\mathrm dy'}{\sinh\!\zeta \,\mathrm dx'+\cosh\!\zeta \,\mathrm d\eta'}=\dfrac{\left(\dfrac{\mathrm dy'}{\mathrm d\eta'}\right)}{\sinh\!\zeta \, \left(\dfrac{\mathrm dx'}{\mathrm d\eta'}\right)+\cosh\!\zeta}
\tag{ft-04b}
\end{align}
From (ft-01) having in mind that $\eta=ct,\eta'=ct'$
\begin{equation}
\dfrac{\mathrm dx'}{\mathrm d\eta'}=0\,,\qquad \dfrac{\mathrm dy'}{\mathrm d\eta'}=\dfrac{u}{c}=\tanh\!\xi
\tag{ft-05}
\end{equation}
Inserting expressions (ft-05) in (ft-04a,b) we have finally
\begin{align}
\dfrac{w_{x}}{c} & =\dfrac{\mathrm dx}{\mathrm d\eta} =\tanh\zeta=\dfrac{\upsilon}{\:\:c\:\:}
\tag{11.1}\\
\dfrac{w_{y}}{c} & = \dfrac{\mathrm dy}{\mathrm d\eta}=\dfrac{\tanh\xi}{\cosh\zeta}=\dfrac{u}{\gamma_{\upsilon}c}
\tag{11.2}
\end{align}
------Figure 06 : The Length------
Figure 07 : The Angle------




