I am interested in a square lattice with the vertical magnetic field. Without a magnetic field, we can know the energy dispersion of the square lattice easily. But, how about in case of with magnetic field? My theory shown below is correct or not?
Without magnetic field
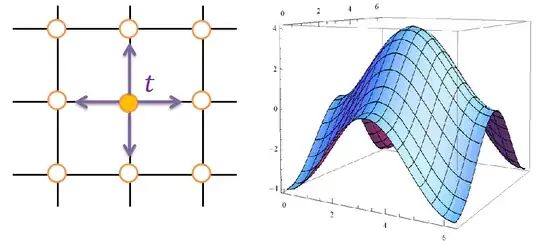
We use tight-binding approximation. We consider only 2Pz orbitals and up to the nearest hopping integral t. Of course, t is a real number. In this case, Hamiltonian matrix is one dimenstional since number of atoms in the unit cell of this system is only one and given by $$ H(k_x,k_y) = te^{ik_xa}+te^{-ik_xa}+te^{ik_ya}+te^{-ik_ya} \\ =2t \cos{k_xa}+ 2t \cos{k_y a}, $$
where a is lattice constant. And we can define wave vector $\vec{k}=(k_x,k_y)$ because system has periodic boundary condition. Right figure is energy dispersion of this system.
With magnetic field
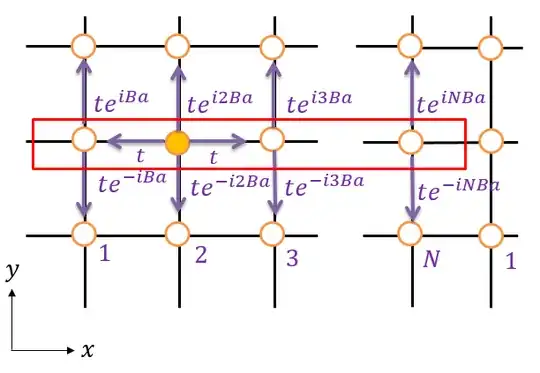
We consider the square lattice with the vertical magnetic field $\vec{B}=(0,0,B)$. We define the vector potential $\vec{A}=(0,Bx,0)$. In this system, transfer integral becomes complex number because of Peierls phase. You know that when we consider magnetic field transfer integral t become $${\rm texp}[i\int_C \vec{A} \cdot d{\vec r}].$$ C is the path of the hopping. In this system, hopping integral of x-direction does not change because $${\rm exp}[(0,Bx,0)\cdot(1,0,0)]=1.$$
But hopping integral of y-direction change and it depends on the x position. This is why the number of atoms in a unit cell becomes N. The red line means unit-cell of this system in the figure. Now, we consider periodic boundary condition in x and y-direction. So,
\begin{eqnarray} te^{i(N+1)Ba}=te^{iBa}. \end{eqnarray}
We can understand $B$ should be satisfied with
$$ B=\frac{2n \pi}{Na} $$
where n is integer.
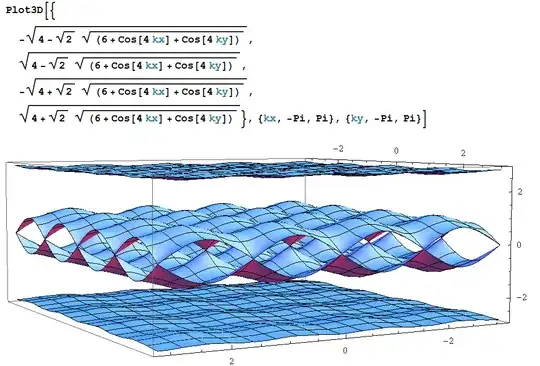
So I made the hamiltonian matrix in case of $N=4$. $$\begin{pmatrix} 2t\cos{(Ba+k_ya)} & te^{ik_xa} & 0 & te^{-ik_xa}\\ te^{-ik_xa} & 2t\cos{(2Ba+k_ya)} & te^{ik_xa} & 0\\ 0 & te^{-ik_xa} & 2t\cos{(3Ba+k_ya)} & te^{ik_xa}\\ te^{ik_xa} & 0 & te^{-ik_xa} & 2t\cos{(4Ba+k_ya)}\\ \end{pmatrix}$$
And according to the Mathematica8, we can know the Eigenvalues analytically, and I plotted it for t=1,a=1 and n=1. So this is energy dispersion of square lattice with magnetic field. Is this correct??
Edit
According to the Mathematica8, when B=0, eigenvalues of the 4-dimensional Hamiltonian are $$ -2t\cos{k_xa}+2t\cos{k_ya}, \\ 2t\cos{k_xa}+2t\cos{k_ya},\\ 2t\cos{k_xa}-2t|\sin{k_ya}|,\\ 2t\cos{k_xa}+2t|\sin{k_ya}|. $$
It is very strange. Why it is not same as the result of the previous section "Without magnetic field"
I found this document. Would you see Fig.2.6? I feel this figure is same as mine.