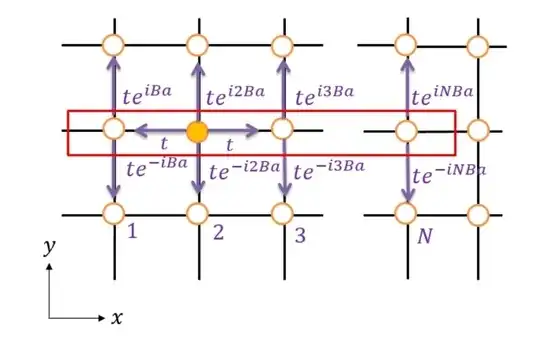
Generalizing the question here, if I have a square lattice in the homogeneous magnetic field $B$ as the given picture, how can we apply the Bloch-Floquet theorem in this periodic structures (with the unit cell which contains $N$ vertices)? As we know, from the Bloch-Floquet theorem, the free ends of a unit cell are related by a phase factor; in this case, this rule applies to which free ends of the cell?
1 Answers
The Hamiltonian of your system can be written as
$$H = t\left[\sum_{n,m} |n+1,m\rangle\langle n,m| + e^{inaB}|n,m+1\rangle\langle n,m| + h.c.\right]$$
Defining the unitary lattice translation operators $T_x = \sum_n |n+1,m\rangle\langle n,m|$ and $T_y = \sum_m |n,m+1\rangle\langle n,m|$, it's easy to show that $T_y HT_y^\dagger= H \iff [T_y,H]=0$. On the other hand,
$$T_xHT_x^\dagger = t \left[\sum_{n,m}|n+1,m\rangle\langle n,m| + e^{i(n-1)aB}|n,m+1\rangle\langle n,m| + h.c.\right]$$ which is generally not equal to $H$ - unless $aB= 2\pi k$ for some $k\in \mathbb Z$. More generally, given any nonzero integer $q$, $$T_x^q H T_x^{q\dagger} = H \iff aB = 2\pi p/q, p\in \mathbb Z$$
where $T_x^{q(\dagger)}=\underbrace{T_x^{(\dagger)}T_x^{(\dagger)}\ldots T_x^{(\dagger)}}_{q\text{ times}}$.
To summarize, your system is generically not periodic unless $\frac{aB}{2\pi} = \frac{p}{q}\in \mathbb Q$ is a rational number (which we take to be in fully-reduced form, so $p$ and $q$ are relatively prime). In that case, the system is periodic with primitive lattice vectors $\mathbf v_x = qa\hat x$ and $\mathbf v_y = a \hat y$.
To apply Bloch's theorem, we should first rewrite our Hamiltonian to explicitly encode our unit cell. In the above, $|n,m\rangle$ refers to the lattice site at position $(na,ma)$. We now define $|N,M\rangle\otimes|\ell\rangle$ to refer to the lattice site at position $\ell$ in the unit cell whose left-most site is at position $(Nqa,Ma)$. In other words, $|N,M\rangle\otimes|\ell\rangle$ refers to the lattice site at position $\big((Nq+\ell)a,Ma\big)$.
From here, our Hamiltonian becomes
$$H = t\sum_{N,M} \left[\sum_{\ell=0}^{q-2} |N,M\rangle\langle N,M|\otimes |\ell+1\rangle\langle \ell|\right.\tag{1}$$ $$ + |N+1,M\rangle\langle N,M| \otimes |0\rangle\langle q-1|\tag{2}$$ $$+ \sum_{\ell=1}^{q-1}\underbrace{e^{i(Nq+\ell)aB}}_{=e^{i\ell aB}\text{ because }qaB\in2\pi\mathbb Z}|N,M+1\rangle\langle N,M| \otimes |\ell\rangle\langle \ell| + h.c.\bigg]\tag{3}$$
The sum in $(1)$ refers to the left-right hopping within a given unit cell. The second term $(2)$ refers to the left-right hopping from one unit cell to the adjacent cell. Finally, the term in $(3)$ refers to vertical hopping between adjacent unit cells.
Having rewritten it this way, we may perform a pseudo-Fourier transform over the unit cell degrees of freedom $|N,M\rangle$ by defining
$$|N,M\rangle = \frac{1}{2\pi}\int \mathrm dk_x \mathrm dk_y \ e^{iNqak_x} e^{iMa k_y} |k_x,k_y\rangle $$ $$|k_x,k_y\rangle = \frac{1}{2\pi} \sum_{N,M} e^{-iNqak_x} e^{-iMak_y} |N,M\rangle$$
where $(k_x,k_y)\in [-\pi/qa,\pi/qa]\times [-\pi/a,\pi/a]$, where the opposite edges of this rectangular region are identified to form a torus. To see why this is necessary, simply observe that $|-\pi/qa,k_y\rangle=|\pi/qa,k_y\rangle$ and $|k_x,-\pi/a\rangle = |k_x, \pi/a\rangle$.
Substituting this into the Hamiltonian, we obtain after some algebra
$$ H = t \int \mathrm dk_x \mathrm dk_y \ |k_x,k_y\rangle\langle k_x,k_y| \otimes h_\mathbf k$$ $$ \mathbf h_k := \left(\sum_{\ell=0}^{q-2}|\ell+1\rangle\langle \ell| + |\ell\rangle\langle\ell+1|\right)\tag{4}$$ $$+e^{iqak_x}|0\rangle\langle q-1| + e^{-iqak_x} |q-1\rangle\langle 0|\tag{5}$$ $$+ \sum_{\ell=0}^{q-1}\underbrace{e^{i\ell aB}e^{iak_y} |\ell\rangle\langle \ell| + e^{-i\ell aB} e^{-iak_y} |\ell\rangle\langle \ell|}_{= 2\cos(\ell a B + a k_y)|\ell\rangle\langle \ell|}\tag{6}$$
This appears to be a horrifying mess, but in fact it's not so bad. For concreteness, let $q=3$ so $h_{\mathbf k}$ is a $3\times 3$ matrix. The terms in $h_\mathbf k$ are respectively:
$$h_{\mathbf k} = \underbrace{\pmatrix{0 & 1 & 0\\1 &0 & 1 \\ 0 & 1 & 0}}_{(4)} + \underbrace{\pmatrix{0 &0 & e^{3iak_x}\\0&0&0\\e^{-3iak_x}&0&0}}_{(5)}+\underbrace{\pmatrix{2\cos(a k_y)&0&0\\0&2\cos(aB + a k_y)&0\\0&0&2\cos(2aB + a k_y)}}_{(6)}$$ $$=\pmatrix{2\cos(a k_y)&1&e^{3iak_x}\\1&2\cos( aB + a k_y)&1\\e^{-3ia k_x}&1&2\cos(2aB + a k_y)}$$
In words, the Hamiltonian has cosines on the diagonal, $1$'s on the adjacent diagonals, and $e^{\pm iqak_x}$ in the upper right and lower left corners, respectively. Further recalling that $aB = 2\pi p/q$, we may write
$$=\pmatrix{2\cos(a k_y)&1&e^{3iak_x}\\1&2\cos( 2\pi p/3+ a k_y)&1\\e^{-3ia k_x}&1&2\cos(4\pi p/3 + a k_y)}$$
This matrix can subsequently be diagonalized to yield the spectrum of the Hamiltonian.
As we know, from the Bloch-Floquet theorem, the free ends of a unit cell are related by a phase factor; in this case, this rule applies to which free ends of the cell?
If I understand what you're saying, the application of the translation operators $T_x^q$ and $T_y$ to an energy eigenfunction $|\psi\rangle = |k_x,k_y\rangle\otimes u_\mathbf k$ (where $u_\mathbf k$ is an eigenfunction of $h_\mathbf k$) yields
$$T_x^q|\psi\rangle = e^{iqak_x}|\psi\rangle\qquad T_y|\psi\rangle = e^{iak_y}|\psi\rangle$$
- 72,909