Interference pattern in delayed choice quantum eraser

Question

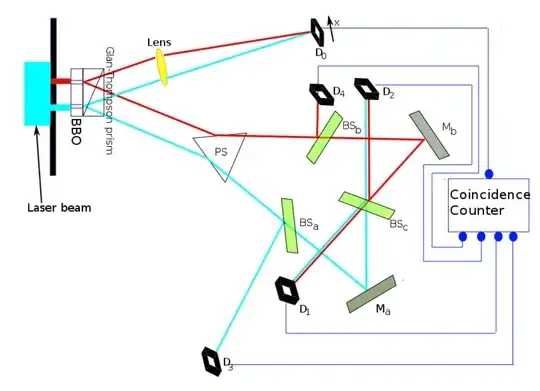
My question is why in the delayed choice quantum eraser experiment we don't see interference pattern at D0? While it looks like it is similar to the normal double slit experiments. The following image is from Wikipedia:

Answer 1

In the usual double-slit experiment the photon is in the superposition of states corresponding to holes A and B. \begin{equation} |DS\rangle=\frac{1}{\sqrt{2}}|A\rangle+\frac{1}{\sqrt{2}}|B\rangle \end{equation} However, in this experiment, the photon then hits the type II BBO crystal which converts it into two photons with perpendicular polarizations. So the state becomes, \begin{equation} |DQE\rangle=\frac{1}{\sqrt{2}}|A,V\rangle_s\otimes|A,H\rangle_i+\frac{1}{\sqrt{2}}|B,V\rangle_s\otimes|B,H\rangle_i \end{equation} It's actually trickier because the BBO produces Bell state $\frac{1}{\sqrt{2}}|V\rangle\otimes|H\rangle+\frac{1}{\sqrt{2}}|H\rangle\otimes|V\rangle$ but in this experiment, we distinguish the photons by polarization so this particular entanglement doesn't play role. Namely the prism sends, say, the one with vertical polarization ("signal") to $D_0$ and the one with horizontal polarization ("idler") to that complex optical system.

The resulting state doesn't factorize into a product of the states of a signal and idler photons $|DQE\rangle\neq|\psi\rangle_s\otimes|\psi\rangle_i$, two photons interfere as a pair but not individually. You may say that the signal photon is marked by a state of the idler photon.

In the formalism that means that we can't assign a pure quantum state (a superposition of some basis quantum states) to a sole photon. Rather if one tries to ignore the idler photon then for the signal photon one gets a so-called mixed state - the $50%$ probability of the state $|A,V\rangle_s$ and the $50%$ probability of the state $|B,V\rangle_s$ without the interference of these outcomes.

How then one gets the interference pattern? We use beam splitters to convert idler photons into superpositions. \begin{equation} |A,H\rangle_i\mapsto \frac{1}{\sqrt{2}}|D_4\rangle_i+\frac{1}{\sqrt{2}}\Big(\frac{1}{\sqrt{2}}|D_1\rangle_i+\frac{1}{\sqrt{2}}|D_2\rangle_i\Big), \end{equation} \begin{equation} |B,H\rangle_i\mapsto \frac{1}{\sqrt{2}}|D_3\rangle_i+\frac{1}{\sqrt{2}}\Big(\frac{1}{\sqrt{2}}|D_1\rangle_i-\frac{1}{\sqrt{2}}|D_2\rangle_i\Big) \end{equation} Note that when the photon arrives at $D_1$ or $D_2$ it's impossible to determine the slit it came from, the state is the same. In this case, we clear which-path information. And as result when we make this transformation in $|DQE\rangle$ we get, \begin{align} |DQE\rangle\mapsto\frac{1}{2}|A,V\rangle_s\otimes|D_4\rangle_i+\frac{1}{2}|A,V\rangle_s\otimes|D_3\rangle_i \\ +\frac{1}{2}\left(\frac{1}{\sqrt{2}}|A,V\rangle_s+\frac{1}{\sqrt{2}}|B,V\rangle_s\right)\otimes|D_1\rangle_i\\ + \frac{1}{2}\left(\frac{1}{\sqrt{2}}|A,V\rangle_s-\frac{1}{\sqrt{2}}|B,V\rangle_s\right)\otimes|D_2\rangle_i \end{align} you may see that if you measure the idler photon either at $D_1$ or $D_2$ you separate the term with the signal photon now being in superposition (note that the phase shifts are chosen to obtain two different superpositions)

Of course, to separate it you need to ignore the events when the idler photon hits $D_3$ or $D_4$. If you sum the statistics at $D_0$ for all four detectors you will recover the initial pattern as if you ignored the idler photon altogether.

Answer 2

@MSH it's similar to the normal double slit experiment when you watch which slit it goes through. The fact that you later erase the which-way information doesn't affect what's detected at $D_0$ by the no-signaling theorem, and a related theorem about unitary operators on just the idler photon.

The only way to get interference back is to use the coincidence detector to look at a subset of detections at $D_0$. The name "quantum eraser", and the emphasis on erasing which-way information, is unfortunate as it obscures the role of filtering, which is essential.

Sabine Hossenfelder has a good video on it, and Sean Caroll a blog post.