As a completely tangential type of answer. Consider a neutron star; due to the General Relativistic bending of light in curved space we are not bounded by the dull constraints of Euclidean geometry!
If the radius falls below 1.76 times the Schwarzschild radius for its mass$^1$, then then all of the surface is visible, when viewed from any direction (e.g. Pechenik et al. 1983; Kraus 1998). Light rays emitted tangentially to the surface from a point on the neutron star that is opposite a (distant) observer would be bent through 90 degrees whilst travelling to the observer. According to that observer, the antipodal point would actually form the circular boundary of the observable disk and hence they could "see" 100% of the surface.
For neutron stars with radii even less than this (as a fraction of the Schwarzschild radius), then there are multiple paths for light to reach the observer for some parts of the surface and they could be seen more than once on the visible disk.
e.g. a neutron star just below the critical $R/R_s$ value where the entire surface can be seen. (From http://www.spacetimetravel.org/ssm/ssm.html )

$^1$ @SeleneRoutley asks whether such objects are theoretically possible or stable? A full answer to this is contained within my response to this Physics SE question, but to summarise:
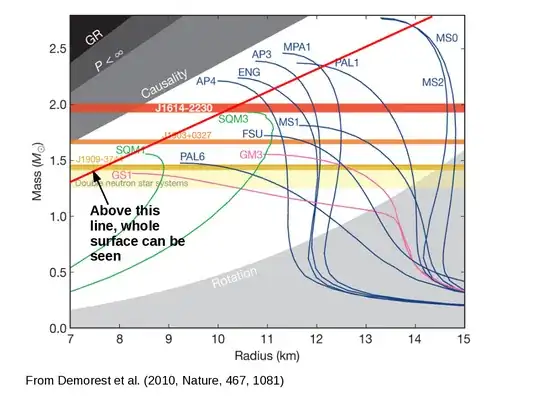
GR does impose a limit on the mass/radius ratio of neutron stars, but the exact limit depends on the equation of state governing the structure. The diagram below shows the theoretical mass-radius plane, adapted from Demorest et al. (2010). The shaded part top-left and marked "Causality" is outlawed by GR and any equation of state where the sound speed is less than the speed of light (as it must be).
I have added a thick red line which marks where the radius equals 1.76 times the Schwarzschild radius. Any neutron star above this line would have a completely visible surface from any viewing direction.
Now there are possible equations of state (marked as labelled loci in this diagram) that allow high-mass neutron stars to exist above the red line. However it is currently not possible to measure the mass and radius of any neutron star with enough accuracy to place them unequivocally above this line, but the measurements for some are consistent with this.
The phenomena discussed above are "routinely" taken account of when inferring spatial structures associated with the pulse profiles of rotating neutron stars at X-ray wavelengths (Sotani & Miyamoto 2018).