Size and density of neutron stars

Question

Most of the books which I looked at give approximately 10 km as the radius of a neutron star. Just yesterday I looked at a book by Dave Goldberg titled The Universe In the Rearview Mirror (2013) which says that they're "only about 5 km in radius" [p.225]. Is this true, [i.e., is there some recent evidence for this], or did he make a mistake here?

Answer 1

10km is about right, 5km is definitely wrong and there are theoretical arguments and also observational evidence that this is the case.

The Schwarzschild radius, inside which an object would be a black hole, is $3(M/M_{\odot})$ km. As neutron stars have a typical mass of $1.5M_{\odot}$ then a 5km radius would have them hovering just above disappearing inside their event horizons.

Now you might have thought that this was possible given a "hard" enough equation of state. But it isn't; there are constraints imposed by general relativity and causality. In "Black Holes, White Dwarfs and Neutron Stars" by Shapiro & Teukolsky, (pp.260-261), it is shown, approximately, that even if the equation of state hardens to the point where the speed of sound equals the speed of light, that $(GM/Rc^2)<0.405$.

The Schwarzschild radius is $R_s=2GM/c^2$ and therefore $R > 1.23 R_s$ for stability. A more accurate treatment in Lattimer (2013) suggests that a maximally compact neutron star has $R\geq 1.41R_s$.

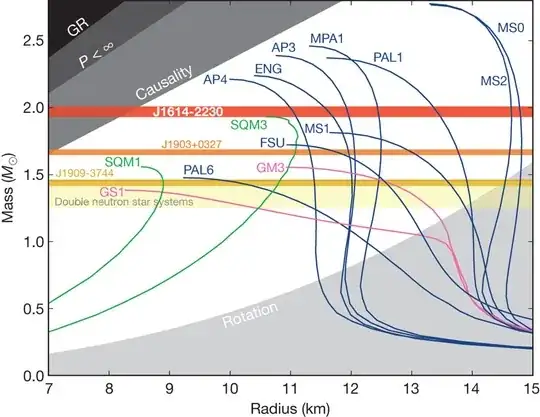
The picture below (from Demorest et al. 2010) shows the mass-radius relations for a wide variety of equations of state. The limits in the top-left of the diagram indicate the limits imposed by (most stringently) the speed of sound being the speed of light (labelled "causality" and which gives radii slightly larger than Shapiro & Teukolsky's approximate result) and then in the very top left, the border marked by "GR" coincides with the Schwarzschild radius. Real neutron stars become unstable where their mass-radius curves peak, so their radii are always significantly greater than $R_s$ at all masses and therefore significantly bigger than 5km for typical neutron stars.

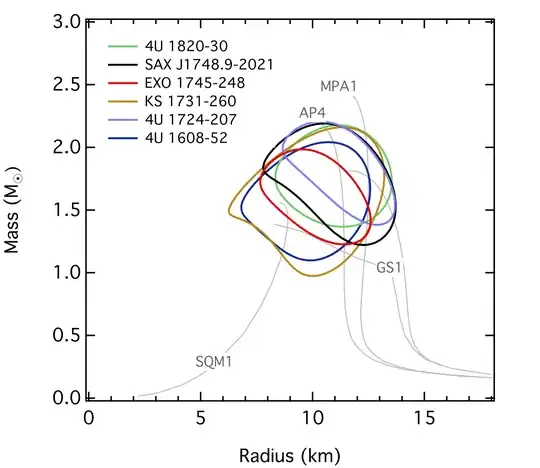
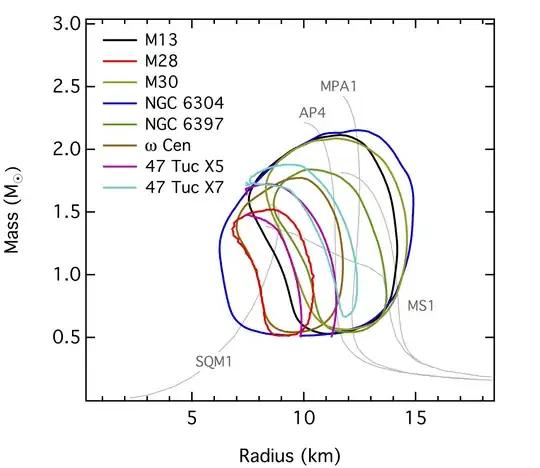
If the theoretical arguments don;t convince then we can look at the best, most recent observational evidence. Ozel et al. (2016) have performed a homogeneous analysis of the X-ray spectroscopy of neutron stars in low mass X-ray binaries: either those that are "bursting sources" or those that are in quiescence. Both cases can be analysed (using different spectral models) to yield both neutron star mass and radii. The constraints are summarised in the plots below. They show that neutron stars do have radii of around 10 km (10.1-11.2 km for neutron stars at $1.5M_{\odot}$).

Radii from bursting LMXBs (from Ozel et al. 2016). 68 percent confidence contours are shown

Radii from quiescent LMXBs (from Ozel et al. (2016). 68 percent confidence contours are shown.

Answer 2

Most of the books which I looked at give approximately 10 km as the radius of a neutron star. Just yesterday I looked at a book by Dave Goldberg titled The Universe In the Rearview Mirror (2013) which says that they're "only about 5 km in radius" [p.225]. Is this true, [i.e., is there some recent evidence for this], or did he make a mistake here?

These are kind of "order of magnitude" estimates determined by balancing neutron degeneracy pressure with the gravitational force exerted by a rough range of stellar masses. Typically, acceptable range of masses results in neutron stars with radii on the order of 10 km (more details below). There have been attempts to confirm this experimentally using Doppler effects on accreting matter and the results are basically consistent with a ~10 km radius. However, when something is several parsecs away it is difficult (but not impossible) to discern the sizes of these objects. Generally we can estimate upper and lower bounds on these objects using physically significant limits/arguments (e.g., the equator probably shouldn't spin faster than the speed of light in vacuum).

Some Example Approximations

The following is largely taken from the book Black Holes, White Dwarfs, and Neutron Stars: The physics of compact objects by Stuart L. Shapiro and Saul A. Teukolsky. There has obviously been a great deal of more recent advances, but this book provides good background and some useful historical context. The below sections are references from the Shapiro and Teukolsky book.

Section 3.4
If one uses the Chandrasekhar limit for an ideal degenerate neutron gas, one finds the maximum mass, $M_{max}$, and radius, $R_{max}$, for a neutron star to be: $M_{max} \sim 1.5 M_{\odot}$ and $R_{max} \sim 3 \ km$, where $M_{\odot}$ is the solar mass. This is the simplest approach, but not really correct.

Section 9.2, Equation 9.2.1
If one assumes a pure, ideal neutron gas and numerically solves the general relativistic equation for hydrostatic equilibrium, one finds: $M_{max} \sim 0.7 M_{\odot}$, $R_{max} \sim 9.6 \ km$, and $\rho_{cr} \sim 5 \times 10^{15} \ g \ cm^{-3}$, where $\rho_{cr}$ is a critical density.

Section 9.2, Equation 9.2.25
A slightly more realisitic ideal gas model includes an equilibrium mixture of non-interacting protons, neutrons, and electrons, which results in: $M_{max} \sim 0.72 M_{\odot}$, $R_{max} \sim 8.8 \ km$, and $\rho_{cr} \sim 5.8 \times 10^{15} \ g \ cm^{-3}$

Section 9.3
The authors go on to discuss even more realistic models all having $M_{max} \lesssim 3 M_{\odot}$ and $5 \ km \lesssim R_{max} \lesssim 15 \ km$.

Section 9.4b, Figure 9.6
The first six observations presented in this section found $1.2 \lesssim M/M_{\odot} \lesssim 1.8$.

Recent Estimates

More recent esimates from observations [e.g., Steiner et al., 2010; 2013] suggest the masses fall in the range $1.4 \lesssim M/M_{\odot} \lesssim 2.2$ and the corresponding radii are $10 \ km \lesssim R \lesssim 13 \ km$.

The most recent paper I found was an arXiv review (i.e., eprint number 1603.02698) provides a nice summary of results where neutron star masses fall in the range $0.5 \lesssim M/M_{\odot} \lesssim 2.5$ and the corresponding radii are $5 \ km \lesssim R \lesssim 15 \ km$.

References

• S.L. Shapiro and S.A. Teukolsky Black Holes, White Dwarfs, and Neutron Stars: The physics of compact objects, John Wiley & Sons, Inc., New York, NY, ISBN:0-471-87316-0, 1983.

Answer 3

5 km in radius seems like a mistake. a 3 solar mass object has a schwarzschild radius of about 9.0 km. (Hence the 10 km estimate for the size of a Neutron star). A little smaller than that and it becomes a black hole.

Also, as I understand it, Neutron stars, like white dwarfs, grow smaller as they add mass. Less massive Neutron stars in the 1.4-1.5 solar mass range should be larger than 10 km in radius which is roughly the size of the more massive ones.