This question is related to Seeing something from only one angle means you have only seen (what?)% of its surface area at most?
Starting from a solid sphere, how can this object be (continuously) transformed so that a viewer (with a single eye) can see most of the surface?
There is no upper limit as we e.g. can transform the sphere to a cone pointing towards the viewer so that the only invisible part is the circular base of the cone and by increasing the height, the portion of this area goes to zero. (and the object moves away to infinity...)
But I somehow feel a bit unsatisfied as this is mathematical perfectly fine, but the angle between the surface normal and the direction towards the viewer goes to 90deg so even if there is nothing blocking the view, the viewer couldn't recognize anything on the surface.
So how does this answer change if we say that the viewing angle is limited?
An (almost) real use case would be a solar collector with a reflective surface so that light that comes in too flat will be rejected and we want to collect as much energy as possible.
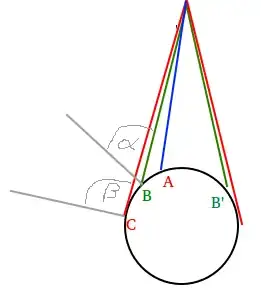
Some Clarification: We have a sphere so without restricting the viewing angle, we see half of the surface. However, at C, the viewing angle beta is almost 90deg, so the resolution of our image of this region gets arbitrary small. So I'd like to select an arbitrary alpha (in the drawing ~60deg) after which a point is no longer considered visible. In this drawing the surface between B and B' (which should be symmetrical) so for the sphere (and this distance to the viewer), around 20% of the surface should be considered visible (or recognizable).