Atomic orbitals and complex wavefunction

Question

I have read different questions related to the atomic orbitals labelled with 2px and 2py present here, such as What is the difference between real orbital & complex orbital? or Notation of complex valued atomic orbitals, but I've not found a complete clarification.

If $px$ and $py$ orbitals are a superposition of two state with definite $m$, which implies that the electron is partially in the $m=+1$ state and partially in the $m=−1$, why it's not so difficult to find books or slides where the $px$ is identified with the quantum number $m=1$ and the $py$ as $m=-1$ like in the image?

It seems that the wavefunction and its modulus squared says something that is similar to this:

So, where is the truth? Why do we need a superposition for the $px$ and $py$ orbitals that doesn't comes out from spherical harmonics, and not for the $pz$?

I'm referring to the hydrogen wave functions:

$$\Psi_{n,l,m} (r, \theta, \phi) = N e^{\frac{-r}{n r_1}} R_n^l (r) P_l^m(cos \theta) e^{im\phi} \,.$$

Answer 1

The truth is your second image:

If you're going to use the magnetic quantum number $m$ as your index, then the $m=\pm 1$ wavefunctions look like rings. A wavefunction with well-defined $m=1$ or $m=-1$ (i.e. an eigenfunction of $\hat L_z$ with eigenvalue $1$ or $-1$) will never have the dumb-bell peanut-like shape of the $m=0$ orbital.

---

Images like the first one, where the $p_x$ and $p_y$ orbitals are identified as having $m=1$ or $m=-1$ are incorrect. Why are they relatively common? Because it's an easy mistake to make - but it doesn't stop it being a mistake.

What the cartesian $p$ orbitals do have is a well-defined $m^2=1$, which is to say, they are eigenstates of $\hat L_z^2$. However, that does not mean that they are eigenstates of $\hat L_z$, which they are not.

(They're also eigenstates of $\hat L_x$ and $\hat L_y$, but that's not a useful characterization - among other things, it does not generalize to higher $m$. If you want a full CSCO description, they're eigenstates of $L^2$, $L_z^2$, and the (commuting) parity operators $\Pi_x$ and $\Pi_y$.)

---

Now, just because they don't have a well-defined $m$, that doesn't mean that they're not useful, either, and for many applications it's more convenient (and perfectly legitimate) to have a real-valued basis set than to have full eigenvector relations for the basis as the $|l,m\rangle$ do (and indeed this is quite common practice in several applications). However, it's perfectly possible to use those orbitals without misrepresenting their relationship with the angular momentum, as your first image does.

Answer 2

During my research pattern on the topic, I have found something that partially answer to my own question and I want to share this with you hoping it can improve the discussion on the topic and help anyone has my same doubt.

I have had the pleasure to read Models, Mysteries and Magic of Molecules book edited by Jan C.A. Boeyens and J.F. Ogilvie in which I have found (Chapter 20) many sentences that widened my horizons such as:

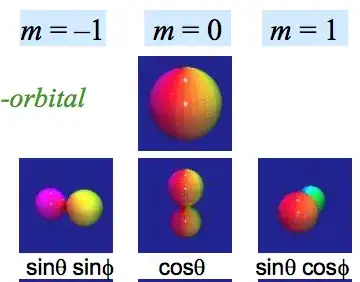
For example, there are three p-type a.o.’s in which the boundary surface consists of two regions together resembling a ′′dumb-bell′′. There is a very marked directional character in these orbitals, which we exhibit by means of a suffix px, py, pz. Chemistry teachers are encouraged to accept this vague picture at face value and to believe that px py pz occurs as a three-fold degenerate solution of Schrödinger’s equation for the H electron. It does not.

---

The linear combinations $\Psi_1 ± \Psi_{-1}$ define one real and one imaginary function directed along the X and Y Cartesian axes respectively, but these functions (denoted $px$ and $ipy$) are no longer eigenfunctions of $L_z$, but of $L_x$ or $L_y$ instead.[...]It is inferred that the vectors $px, py, pz,$ like $L_x$, $L_y$ and $L_z$ do not commute and cannot be simultaneous solutions.

---

As shown already, the linear combinations that define px and py are simple rotations of the coordinate axes. It follows that the functions px and py are both characterized by the quantum number m = 0 that defines zero component of angular momentum, now directed along the Cartesian X and Y axes respectively.[...]These ′′orbitals′′ can never occur together.

---

It has become general practice in chemistry to refer to the presumed polar density distribution for $m_l = 0$ as a pz-orbital. Should the coordinate axes be relabeled, this entity should also be relabeled as either px or py. It is physically meaningless to specify two of these orbitals at the same time.

---

Statement as "the three p orbitals are directed along the three Cartesian axes and will tend to form bonds in these directions" are all based on the same false premises that the pair of real functions $px$ and $py$, are equivalent to the complex pair $e^{±i \phi}$

---

Despite the fact that the physics of atomic structure therefore militates against a $px py pz$ set of electrons on the same atom, it may be (and often is) argued that, since each of the three eigenfunctions, separately, solves the atomic wave equation, a linear combination of the three must likewise be a solution of the same equation. Formation of such a linear combination is a purely mathematical procedure without any reference to electrons. It simply is a manipulation of three one-electron eigenfunctions and it is of interest to examine what physical meaning attached to the operation.

---

The important conclusion is that each linear combination corresponds to a new choice of axes.

---

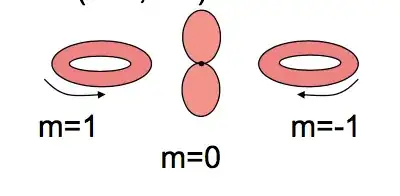
So from the previous and many other statements, it seems that only one orbitals can have "dumb-bell" shape at time, while the other two ones have the shapes represented by the second image.

Beyond any other mathematical explanation (it's obvious that a superposition of wavefunction is still a Schrödinger's equation solution), what is important to me is the physical meanings of this operations.

Hoping this can help, any other suggestions are accepted.