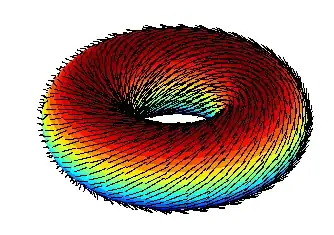
The concept of a spherical electromagnetic wave is a nice fiction, which is sometimes called upon in introductory optics textbooks, but it runs into a deep topological problem in the form of Brouwer's hairy ball theorem, which essentially states that
if $\mathbf f:\mathbb S^2\to\mathbb R^3$ is a continuous function that assigns a vector $\mathbf f(p)$ in $\mathbb R^3$ to every point $p$ on a sphere such that $\mathbf f(p)$ is always tangent to the sphere at $p$, then there is at least one $p$ such that $\mathbf f(p) = 0$,
or, in other words, "you cannot comb a hairy sphere". As regards electromagnetism, this means that a linearly-polarized spherical wave cannot be isotropic, because Gauss's law requires the radiation component to be transverse, and the hairy-ball theorem then requires it to have zeroes in its angular intensity distribution.
The usual argument with e.g. stars and the like is that the radiation they emit is not coherent, which sidesteps this limitation. However, a recent answer pointed out that if you relax the requirement that the polarization be uniform, it becomes possible to have coherent spherical waves with an isotropic intensity distribution by letting them take elliptical or circular polarizations over some directions, and that is plenty interesting in its own right. However, this is not a point that is made very often, so I would like to see explicit forms of how this can be done.
More specifically, I would like to see explicit exact solutions of the vacuum Maxwell equations on full space minus a sphere, i.e. $\{\mathbf r\in\mathbb R^3:\|\mathbf r\|>a\}$, which are (i) monochromatic, (ii) outgoing spherical waves, and (iii) have constant intensity over every sphere centered at the origin. If there is an explicit decomposition of this wave into e.g. a sum of two orthogonal linear polarizations with different intensity distributions, that would be good to see as well.
I believe the references in the previous answer, including this, can be worked into that form with some ease, but I'm not particularly fussed about the existence of easy implementations with straight-wire antennas or anything like that - I would value more solutions that are exact everywhere over solutions that have the desired properties in an asymptotic sense. That said, if there is a current distribution on the sphere itself that will give the desired solutions exactly (in the sense of this answer), then that's certainly interesting.