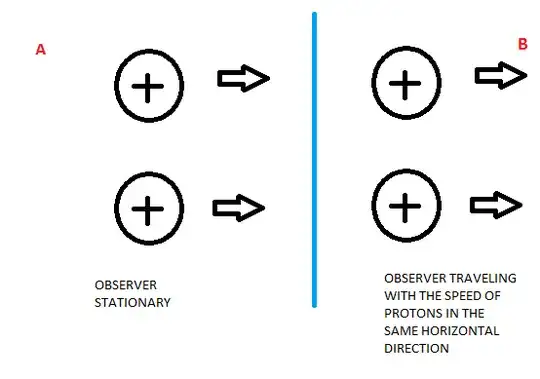
The question I have about it is how we can get the same result of net force acting on the individual protons if we judge the system from 2 different reference frames. One using more of the magnetic part of the electromagnetism, other more of electrical part of it to calculate the forces.
So I'll try to explain my understanding of it trough these two examples in which I get different results of particle acceleration depending on the different reference frames named in the Picture as "observer reference frames".
For simplicity I've decided to ignore the magnetic field created by the particles spins. I think they do not matter for this mental excercise.
In example A, both protons are traveling in the same direction and with the SAME speed. If the observer is stationary, he sees both of them moving away from him at the same speed. Because the protons have the same charge, they are repelled away from eachother by electrostatic force. But because they are moving, the upper proton creates a magnetic field around itself and that field acts on the other proton in such a way to push him up (towards the other proton). The same is true for the other proton which magneticaly attracts the other proton. The direction net force is dependant on the speeds of protons and how far away from eachother they are. So in one case they might attract eachother (high speeds) and in other case repel (close together).
Now let's look at example B. The observer is traveling at the same speed as the protons and in the same direction. The protons according to the observers aren't moving. So magnetic force doesn't appear between the protons. The only thing the protons feel according to the observer is the repulsive electrostatic force between them, so the protons, no matter how far away from eachother they are or at what velocity they are traveling (according to the stationary observer from case A) Will always repel eachother.
Now this entirely contradicts itself. Does this have something to do with time dilation and space contraction effects? And if so, how?
I've read the examples of a current conducting wire and it's effect on a moving independant charge. That picture makes sense because of space contraction, so there are more of opposite (stationary) charges in the same volume of space (in a wire) than if the charges weren't moving relative to eachother. That creates an electrostatic force which can in different reference frame be considered a magnetic force. But here we do not have the "help" from those opposite charges. And I believe the same effect still occures. How?