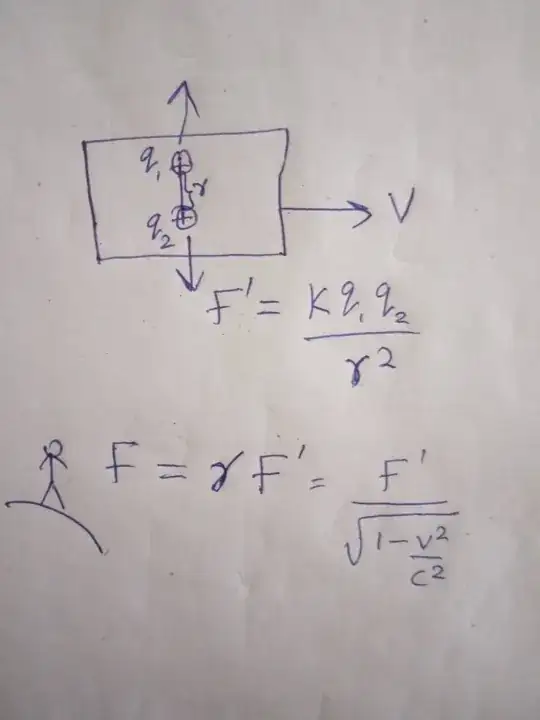
A common class of error, in these sorts of problems, is getting the transformation backwards and putting $\gamma$ where you should have $1/\gamma$. That's what's happened to you here.
To see this intuitively, consider a pair of opposite charges instead of same-sign charges. Released from rest, the opposite charges will accelerate towards each other and collide after some finite time. An observer in a different frame will see this collision happen more slowly, due to time dilation.
How the moving observer explains this delayed collision is sensitive to the geometry of the problem. If the line between the charges is perpendicular to the velocity, as in your diagram, the moving observer believes there is a magnetic interaction between the charges which counteracts their electrical attraction. (A classic problem from Griffiths: consider parallel line charges, and find the speed at which the magnetic repulsion exactly cancels the electrical attraction.) If the line between your point charges were parallel to the velocity vector, there would be zero magnetic force between them, but the electrical attraction would have been reduced thanks to the Lorentz boost. At other angles, the boosted electrical force and the magnetic interaction conspire together so that your opposite charges collide after exactly the right dilated amount of time.