Multiple colliding balls

Question

I have written an algoritm to resolve a collision between two balls with conservation of momentum. It looks to work exactly as expected in my simulations. Here is the code:

public void Resolve()
{
  var r = 0.5; // coefficient of restitution
  var m = Ball1.Mass + Ball2.Mass;
  var ua = Ball1.Velocity.Magnitude * Math.Cos(Ball1.Velocity.Angle(Normal));
  var ub = Ball2.Velocity.Magnitude * Math.Cos(Ball2.Velocity.Angle(Normal));
  var va = (r * Ball2.Mass * (ub - ua) + Ball1.Mass * ua + Ball2.Mass * ub) / m;
  var vb = (r * Ball1.Mass * (ua - ub) + Ball1.Mass * ua + Ball2.Mass * ub) / m;
  Ball1.Velocity -= Normal * (ua - va);
  Ball2.Velocity -= Normal * (ub - vb);
}

Now I also want to make this work for more than two balls colliding at the exact same moment. My initial thought was that I could just solve this equation several times for each contact between balls. When I have a situation like a "Newton's cradle" where the balls is in contact in a "serial" way it's easy to just solve each collision on at a time and without moving the balls just go ahead and calculate the next and the next etc until reaching the last ball which will end up with all energy not lost along the way. This works fine also, albeit not very fast.

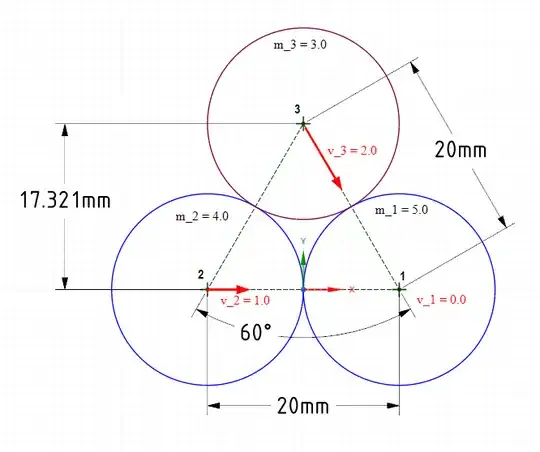
But what about for instance a case where three balls are in contact in a V-shape and the bottom ball is the one with a velocity (up in this case)? I mean how now do I distribute the energy between the other two balls? The equation I have only works for two balls and now I don't see how I can calculate this iteratively anymore. Can you help guide me in how I should think with this? Can I modify my Resolve-function to work with any number of balls? I mean with a set of $N$ balls with connecting surfaces and initial velocity vectors, what will the outcome velocities be? Is there a well known general solution for this?

Note:

I have tried out the method currently marked as the answer but I have unfortunately got a bit weird results in some setups. Be warned. I will probably revert back to resolving one collision at a time again. I will update this info when I have tried this more.

Answer 1

You need to setup a system of $K$ equations with $K$ impulse unknowns if derived from the $N$ balls whereas only $K$ of them are colliding at some time.

Here is how to do it:

1. Create a (block) vector with all velocity vectors in sequence. The size is $2N\times1$ $$ \mathbf{v} = \begin{pmatrix} \vec{v}_1 \\ \vec{v}_2 \\ \vdots \\ \vec{v}_N \end{pmatrix} = \begin{pmatrix} \dot{x}_1 \\ \dot{y}_1 \\ \dot{x}_2 \\ \dot{y}_2 \\ \vdots \\ \dot{x}_N \\ \dot{y}_N \end{pmatrix} $$

2. Create a (block) matrix with all the masses, but also of $2N$ rows $$\mathbf{M} = \begin{bmatrix} m_1 & 0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & m_1 & 0 & 0 & & 0 & 0 \\ 0 & 0 & m_2 & 0 & & 0 & 0 \\ 0 & 0 & 0 & m_2 & & 0 & 0 \\ & & & & \ddots & & \\ 0 & 0 & 0 & 0 & & m_N & 0 \\0 & 0 & 0 & 0 & & 0 & m_N \end{bmatrix}$$ such that $\mathbf{M} \mathbf{v}$ would be all the momentum componnets.

3. You are looking for the change in velocity $\Delta \mathbf{v}$ due to all the impulses from the collisions. If you knew the sum of all impulses $\boldsymbol{\ell}$ (again in $2N\times1$ vector) then you would write the change in velocity as $$\Delta \mathbf{v} = \mathbf{M}^{-1} \boldsymbol{\ell}$$

4. Create a $2N \times K$ contact pair block matrix $\mathbf{Z}$. Each column represents a contact between two bodies ($i \rightarrow j$) by containing the contact normal vector $\hat{n}_{ij}$ in the $j$-th block position, and the negative normal vector $-\hat{n}_{ij}$ in the $i$-th block position. For example: $$\mathbf{Z} = \begin{bmatrix} -\hat{n}_{13} & 0 & -\hat{n}_{14} \\ 0 & -\hat{n}_{24} & 0 \\ \hat{n}_{13} & 0 & 0 \\ 0 & \hat{n}_{24} & \hat{n}_{14} \end{bmatrix}$$ represents the contact pair matrix when bodies ($1 \rightarrow 3$, $2 \rightarrow 3$ and $1 \rightarrow 4$) are colliding. The arrow indicates the direction at which the normal vector points, and hence the direction where the positive impulse is applied. Remember that each contact normal vector has two components $\hat{n} = ( \cos \psi, \sin \psi )$.

5. Construct a $K \times 1$ vector of unknown impulse magnitudes for each contact pair. $$ \mathbf{J} = \begin{pmatrix} J_{13} \\ J_{24} \\ J_{14} \end{pmatrix}$$ Now the sum of all impulses are computed by $$\boldsymbol{\ell} = \mathbf{Z} \,\mathbf{J}$$

6. Calculate the relative speed of each contact pair ($K \times 1$ vector) by projecting the speeds along the contact normal $$ \mathbf{u}_{imp} = \mathbf{Z}^\top \mathbf{v}$$

7. Establish the law of collision in terms of the relative speeds before and after the collision. $$ \mathbf{Z}^\top \left( \mathbf{v} + \Delta \mathbf{v} \right) = -\epsilon \mathbf{Z}^\top \mathbf{v}$$ where $\epsilon$ is the coefficient of restitution. Move the knowns to the right hand side and find the change in relative speeds by $$ \mathbf{Z}^\top \Delta \mathbf{v} = -(1+\epsilon) \mathbf{Z}^\top \mathbf{v} = -(1+\epsilon) \mathbf{u}_{imp}$$

8. Put 3. 5. and 7. together to make $$ \mathbf{Z}^\top \left(\mathbf{M}^{-1} \left( \mathbf{Z} \,\mathbf{J} \right) \right) = -(1+\epsilon) \mathbf{u}_{imp} $$ and solve for the unknown impulses $$ \mathbf{J} = -\left(\mathbf{Z}^\top \mathbf{M}^{-1} \mathbf{Z} \right)^{-1} (1+\epsilon) \mathbf{u}_{imp} $$ Note that $\mathbf{Z}^\top \mathbf{M}^{-1} \mathbf{Z}$ is a $K \times K$ matrix that needs inversion.

9. When all the impulses are calculated, each body velocity vector changes by $$ \Delta \mathbf{v} = \mathbf{M}^{-1} \mathbf{Z} \,\mathbf{J} $$

Example

Imagine three spheres impacting at the same time:

Use this MATLAB script to find their final velocties:

%% Example triple impact (with 3D vectors)
% Three spheres impact at the same time. See Figure for their
% masses, positions and velocities before impact

% define unit vectors
o_ = [0;0;0];
i_ = [1;0;0];
j_ = [0;1;0];
k_ = [0;0;1];

R = 20;
r_1 = R*i_ 
r_2 = -R*i_
r_3 = R*tand(60)*j_

% Three possible contacts: 1*2, 2*3, 1*3
n_12 = (r_2-r_1)/norm(r_2-r_1)
n_23 = (r_3-r_2)/norm(r_3-r_2)
n_13 = (r_3-r_1)/norm(r_3-r_1)

% velocity vectors before impact
v_1 = o_;
v_2 = -1.0*n_12
v_3 = -2.0*n_13

v = [v_1;v_2;v_3]

% mass matrix
M = blkdiag(5.0*eye(3),4.0*eye(3),3.0*eye(3))

% contact pair matrix
Z = [-n_12, o_, -n_13; n_12, -n_23, o_; o_, n_23, n_13]
% Z =
% 
%     1.0000         0    0.5000
%          0         0   -0.8660
%          0         0         0
%    -1.0000   -0.5000         0
%          0   -0.8660         0
%          0         0         0
%          0    0.5000   -0.5000
%          0    0.8660    0.8660
%          0         0         0

% coefficient of restitution
eps = 0.5

% impact speeds
u_imp = Z.'*v

% impulses
J = -(1+eps)*inv(Z.'*inv(M)*Z)*u_imp
% J =
% 
%     1.7021
%     2.1702
%     4.6277

% velocity vector change
Dv = inv(M)*Z*J

% final velocity
v_final = v+Dv
% v_final =
% 
%     0.8032
%    -0.8015
%          0
%     0.3032
%    -0.4699
%          0
%     0.5904
%     0.2303
%          0


% check for error
actual = Z.'*(v+Dv);        %(relative speeds after impact) =
expected = -eps * u_imp;    % -eps*(relative speeds before impact)
err = actual-expected

% err =
% 
%   1.0e-015 *
% 
%    -0.1110
%    -0.6661
%    -0.6661

In the last part, I check the results against the law of contacts and the error is ~1e-15.

Answer 2

Unfortunately I have to agree with Jonathan Wheeler : There are no other formulas available, and your current method is probably the best there is even for only 3 balls.

In Newton's Cradle, the outcome is the same whether the balls are touching or not. A slight gap between balls gives the same final result. This suggests that your approach of splitting the multiple-body collision into a succession of pair-wise collisions will give the correct physical result. This is almost always possible in practice because if the resolution is increased - ie the time-step in the simulation is reduced - then one pair-wise collision can be seen to occur first.

The downside, as you have noted, is that this procedure may require excessive computation, because there could be many re-collisions between the same pair of bodies. If the simulation is being displayed in real time, the whole simulation could be slowed down noticeably whenever such a collision occurs. Hence the need for a method of deciding the outcome without so much iteration.

Except in a few situations in which there is some symmetry, there is (as far as I am aware) no known closed formula giving the result even for a 3-body collision, comparable with equations for the 2-body collision. This is because the simultaneous collision of 3 rigid-bodies is indeterminate - ie there are not enough constraints to match the number of variables.

As garyp suggests, including elastic deformation and forces in the model provides more constraints, enabling the outcome to be determined. However, modelling deformable bodies adds to the complexity of the program, and because of the coupling between forces the resulting equations are likely to require numerical solution by iteration. So the same problem of an increased computation time arises.

Symmetrical collisions of 3 identical balls include (i) the co-linear case, and (ii) one ball travelling perpendicular to the other 2, which are either stationary or move with the same velocity in the same or opposite direction to the 1st. However, such symmetrical cases will be extremely rare in a molecular motion type of simulation.

Conclusion: If you want your simulation to be an accurate depiction of a real 3-body collision, your current method (solving successive pair-wise collisions with sufficient time-resolution) is probably the most efficient available. The same method handles all multiple-ball collisions.

---

Useful references

Question regarding elastic collisions and the conservation of momentum / energy
Rigid body collision, 3 circles in contact
Calculating a 3 way circle collision

Research Articles

A propagative model of simultaneous impact: existence, uniqueness, and design consequences
Reflections on Simultaneous Impact
Making a meaningful impact : modelling simultaneous frictional collisions in spatial multibody systems
Newton’s cradle undone: Experiments and collision models for the normal collision of three solid spheres (access via paywall)
The Two Ball Bounce Problem
A State Transition Diagram for Simultaneous Collisions with Application in Billiard Shooting
Restitution properties in direct central collision of three inelastic spheres
Two Interpretations of Rigidity in Rigid Body Collisions (ResearchGate listing with citations)

Answer 3

This is only a partial answer, but hopefully it will help.

There are two principles that you need to keep in mind when you're solving for motion. Conservation of Energy and Conservation of Momentum. Namely,

$$ (m_1 v_1^2 + m_2 v_2^2 + m_3 v_3^2)_\text{before} = (m_1 v_1^2 + m_2 v_2^2 + m_3 v_3^2)_\text{after}$$

$$ (m_1 \mathbf{v_1} + m_2 \mathbf{v_2} + m_3 \mathbf{v_3})_\text{before} = (m_1 \mathbf{v_1} + m_2 \mathbf{v_2} + m_3 \mathbf{v_3})_\text{after} $$

In general, the 'three body' problem is quite hard to solve, and if you can, you may be better off modeling the collision of three balls in three pairs of collisions. I don't think that solving these conservation equations above will lead to any elegant formal when $n \ge 3$.