Ball A (2 kg) is moving towards ball B (1 kg) at 4 m/s. On the other side, ball C (7 kg) is moving towards ball B at 3 m/s. If all three balls collide elastically at the same time, what is the final velocity of each ball? This is a one-dimensional system with no spin, and the coefficient of restitution is 1.
I've tried having the balls collide one at a time, but I got different answers when A and B collide first and when B and C collide first.
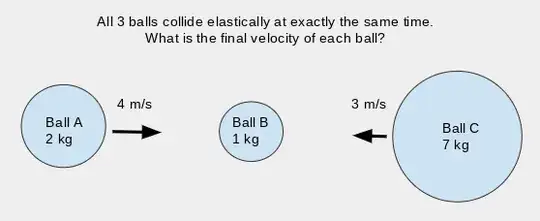
You have to consider two impulses hitting mass B at the same time. If the impact between AB exchanges momentum (impulse) of magnitude $J_{AB}$ and the impact between BC exchanges momentum (impulse) of magnitude $J_{BC}$ then the change in velocities are
$$ \begin{aligned} \Delta v_A & = \frac{-J_{AB}}{m_A} \\ \Delta v_B & = \frac{J_{AB}-J_{BC}}{m_B} \\ \Delta v_C & = \frac{J_{BC}}{m_C} \end{aligned}$$
Now use the above in the law of contact that relates the final velocities to the initial velocities
$$ \begin{aligned} (v_A + \Delta v_A) - (v_B + \Delta v_B) & = -\epsilon (v_A-v_B) & &\mbox{A to B contact}\\ (v_B + \Delta v_B) - (v_C + \Delta v_C) & = -\epsilon (v_B-v_C) & &\mbox{B to C contact}\\ \end{aligned}$$
Where $\epsilon=1$ is the coefficient of restitution.
These are two equations to be solved for the two unknown impulses, $J_{AB}$ and $J_{BC}$.
$$\begin{aligned} J_{AB} & = (1+\epsilon) \frac{ m_A m_B (v_A-v_B) + m_A m_C (v_A-v_C)}{m_A+m_B+m_C} \\ J_{BC} & = (1+\epsilon) \frac{m_A m_C (v_A-v_C) + m_B m_C (v_B-v_C)}{m_A+m_B+m_C} \end{aligned}$$
Finally use these the first set of expressions to find the change in velocities.
First consider momentum conservation at the moment of collision, Consider the left direction to be positive and we get the total momentum to be 21-8 = 13kgms^-1 Now let the final velocity of ball A to be X, B to be Y, C to be Z. 2x + y + 7z = 13 Next consider each collision, rearranging the coefficient of restitution equation gives us -4 + x = 0 + y similarly 3 + Z = 0 + y
Since we have 3 variables and 3 equations, we can solve this and find each value X,Y,Z
Said another way:
1) Speed of separation = Speed of approach - for all three bodies, relative to the center of mass of the system (and each other) because the collision is elastic (and KE is conserved).
2) The velocity of the center of mass of the system (Vs) remains unchanged, by conservation of momentum.
From IK-_-IK's answer, Vs = -1.3 Some addition gives final velocities of: A = -6.6 B = -2.6 C = .4
These numbers solve IK-_-IK's equations too, so I'm not sure where you went wrong with analyzing the collision as if it was a series of two body collisions, but I believe it should work that way too. If it doesn't, that is very counter intuitive.
