1

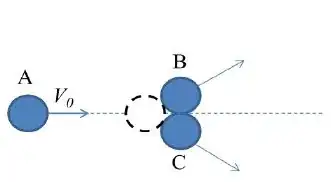
I've been working on this question for a few hours and I cannot quite convince myself that my answer is correct. I've read the relevant section in my textbook, but I guess the lightbulb just isn't clicking on. The question (which I'll post the full text of below), asks for final velocity of a puck in three body collision in which two of the bodies are initially at rest. I was thinking that, since I only need final velocity, I could just use the conservation of linear momentum in the relevant plane (since this equation has a term for v) and solve it out for v. Other solution I've seen use both linear momentum AND conservation of energy equations. Which way is correct? See picture for question and attempted solution. Any help is greatly appreciated.

Question: Three identical round pucks A, B, and C are placed on frictionless surface as shown. The puck A is shot with initial velocity V0 along the symmetry line. The pucks B and C are initially touching each other. The pucks undergo elastic collision. This question asks that I find the final velocity of Puck A.

EDIT: My attempt is included in the image below. The problem I'm currently having is that I'm not sure if I can treat Pucks A & B as a single object for the purposes of this solution.

Pic enter image description here

PhysicsStudent
  • 21

2 Answers2

0

You will agree that the velocity of A depends on the elasticity of the collision. Now, momentum is conserved regardless of the elasticity of the collision. Therefore, you cannot expect momentum conservation alone to determine the outgoing velocity of A.

In detail, the total outgoing momentum depends on two unknowns, i.e. A's velocity and B and C's common velocity. You need an extra equation to uniquely determine your solution, and that is what energy conservation does.

Arek' Fu
  • 119
0

Assume all masses are the same and we have a perfectly symmetrical collision. It seems a logical assumption doesn't it? Then, try to understand the following conservation of energy equation. Use it to solve for $v_{af}$:

$$\frac{1}{2}mv_{ai}^2 = \frac{1}{2}mv_{af}^2 + \frac{1}{2}mv_{b}^2 +\frac{1}{2}mv_{c}^2$$

Once you've done that, go back and solve the problem using conservation of momentum. That's trickier because you have to remember that you can have conservation of total momentum, you can have conservation of momentum in the $x$-direction, and you can have conservation of momentum in the $y$-direction. You will also have to handle the angles in order to solve it with conservation of momentum. Good luck!

Inquisitive
  • 1,651
  • 9
  • 13