I'm trying to answer the following question which was asked in the theoretical minimum exam composed by Lev Landau.
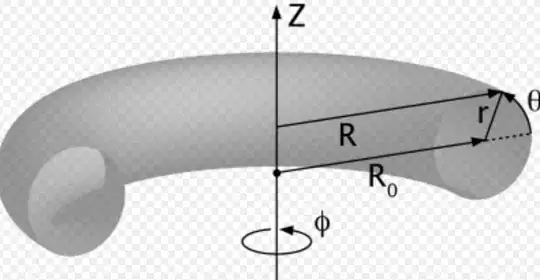
The electron enters a straight pipe of circular cross section (radius $r$). The tube is bent at a radius $R\gg r$ by the angle $\alpha$ and then is aligned back again. Find the probability that the electron will jump out.
Here is my attempt:
As mentioned in the question, the tube is bent and assuming that this action takes place after the electron's entry, the tube would oscillate with a specific frequency after its release, this frequency would depend upon properties of the tube and it's gravitational potential. The depression of the loaded end is
 $$\xi=\frac{Mg}{YI}\left(\frac{l^3}{3}\right)$$, hence the restoring force is proportional to the depression. The frequency of oscillations is hence,$$f=\frac{1}{2\pi}\left(\frac{3YI}{Ml^3}\right)^{\frac{1}{2}}$$
With this being said how can I construct a potential that oscillates with such a frequency? I ask this because if there is an oscillating potential barrier for the electron, which(the potential) has its peaks higher than the electron's Energy and allows transversal motion of the electron only when the potential reaches a minima;hence making the electron move in small steps. Below I have written down the strain and gravitational potential energies and used them in the Schrödinger equation as the associated wavefunction gives the probability of finding a particle at a certain position.
$$\xi=\frac{Mg}{YI}\left(\frac{l^3}{3}\right)$$, hence the restoring force is proportional to the depression. The frequency of oscillations is hence,$$f=\frac{1}{2\pi}\left(\frac{3YI}{Ml^3}\right)^{\frac{1}{2}}$$
With this being said how can I construct a potential that oscillates with such a frequency? I ask this because if there is an oscillating potential barrier for the electron, which(the potential) has its peaks higher than the electron's Energy and allows transversal motion of the electron only when the potential reaches a minima;hence making the electron move in small steps. Below I have written down the strain and gravitational potential energies and used them in the Schrödinger equation as the associated wavefunction gives the probability of finding a particle at a certain position.
The potential strain energy of a bending tube is: $$V_{b}=\frac{M\alpha}{2}$$ Since, $\alpha$ is related to the moment as:$\alpha=\frac{ML}{2YI}$, where $Y$ is the Young's modulus and I is the moment of inertia($I=\frac{Mr^2}{2}$), we can rewrite the potential equation as: $$\boxed{V_{b}=\frac{RM\alpha}{Yr^2}}$$ Now since there is also a gravitational potential associated with the bent tube, it can be written as follows: $$\boxed{V_{g}=\frac{2GM\sin\left(\frac{\alpha}{2}\right)}{R\alpha}}$$
I now introduce toroidal coordinates,where $\tau=\ln\frac{d_{1}}{d_{2}}$(please refer to the wiki link), here since $d_{1}=d_{2}$, $x=y=0$, and $$z=\frac{a\sin\alpha}{1-\cos\alpha}=\frac{R^{2}\sin(\alpha)\left(1-\frac{r^{2}}{R^{2}}\right)}{\left(4R^{2}+4\frac{r^{4}}{R^{2}}-8\frac{r^{2}}{R^{2}}-1\right)}$$ Where $a=R^{2}-r^{2}$ and $\cos\alpha=-\frac{\left(4a^2-2R^{2}\right)}{R^{2}}$
Now these potentials can be incorporated into the Schrödinger time independent as the associated wavefunction gives the probability of finding the particle at a certain position: $$\boxed{\frac{\mathrm d^{2}\psi}{\mathrm dz^{2}}=-~\frac{2m}{\hbar^{2}}\left(E-\frac{RM\alpha}{Yr^2}-\frac{2GM\sin\left(\frac{\alpha}{2}\right)}{R\alpha}\right)\psi(z)}$$
As observed from the above equation the gravitational potential energy oscillates sinusoidally, but how am I to construct a potential with the frequency I mentioned above. Am I right to assume the above potentials for solving this problem? If yes, how do I proceed further? Any help is appreciated.
edit: I have proceeded to answer by the above method as nothing is explicitly mentioned in the question as of how to go about solving it. I got this question from here. I would also like to add that the above method I have used may be one where I am just complicating a simple problem, I may be wrong but not the question, I beg to differ as I believe that such a problem asked by Landau would not have a simple solution given that only 45 students ever passed the theoretical minimum.