What's at the very center of a Black Hole?

Question

I understand General Relativity predicts a singularity. A theory of Quantum Gravity must surely change that. Based on some very simple considerations I predict the central core is a "condensate" of neutral spin 1/2 particles. But my simple considerations have one unfortunate drawback.. they also predict a violation of the law of conservation of angular momentum. So, what's the current thinking about the very center of a black hole.

Answer 1

This question is a bit strange. I wrote a post here on the singularity of a rotating black hole or the Kerr metric. I will refer to that some in trying to address this question. I will not entirely say what the singularity is, but offer some thoughts which may motivate questions and additional ideas. I will use a number of diagrams and illustrations, rather than mathematical pedantry.

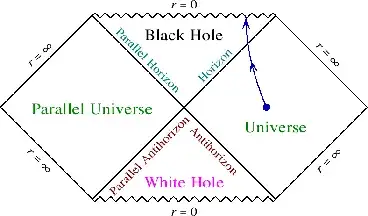
A comment is made that this fails to specify what theory is used, but the one problem is that we do not have much real theory here. I put here a conformal diagram of the Schwarzschild metric

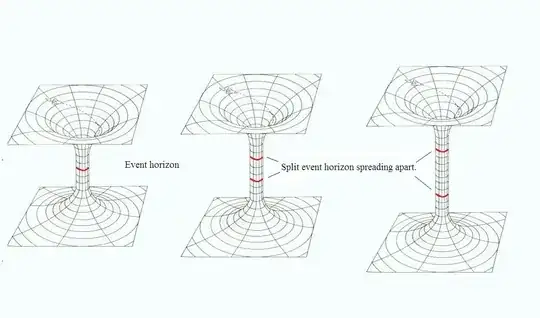
The point where the horizon splits is the region on the horizon for the coordinate origin of an external observer at constant distance from the horizon. This horizon in the black hole region is split and to the observer entering the black hole the horizons separating two exterior regions or universes fly apart at the speed of light. I include below a diagram with black hole "well" and the horizon moving apart

The two horizons spread apart and reach their maximum separation at $r~=~0$. At that point the observer reaches a spatial surface of large, or infinite in the case of an "eternal black hole," where the Weyl curvature becomes arbitrarily large or divergent.

What happens at this singularity is a bit speculative. Curmrun Vafa with mirror symmetry illustrates that this singularity is a condensate of tachyons. This has some plausibility to it for the singularity as some quantum physical system is atemporal on a spatial surface, which is similar to a tachyon. We might review what a tachyon is. This is a case where the invariant momentum interval $$ (mc^2)^2~=~E^2~-~(pc)^2~<~0, $$ which is interpreted as meaning the particle is traveling faster than light and is on a spacelike interval. This is on motivating reason to think the quantum singularity may be tachyonic, or a condensate of tachyons. There is another motivating reason; it is an unstable vacuum. A scalar field $\phi$ with $m^2~<~0$ has the Lagrangia $$ L~=~\frac{1}{2}\partial_\mu\phi^*\partial^\mu~-~\frac{1}{2}m^2\phi^*\phi, $$ where $m^2\phi^*\phi$ is the potential. However, if this is negative it means all states including the vacuum are not stable and run-away in a divergent manner. $$ \nabla^2\phi~-~\frac{\partial\phi}{\partial t}~+~m^2\phi~=~0. $$ The potential gives a "force" $m^2\phi$ that drives in a positive feedback manner the magnitude of the scalar field and causes it to "explode."

Referring to black holes again, let us look at the conformal metric for the black hole which considers the case with Hawking radiation. I refer to the diagram below

Here it is evident the singularity as the spacelike region at $r~=~0$ is coincident with the evaporation of the black hole as seen from the exterior. The singularity is then an unstable configuration of fields associated with Hawking radiation.

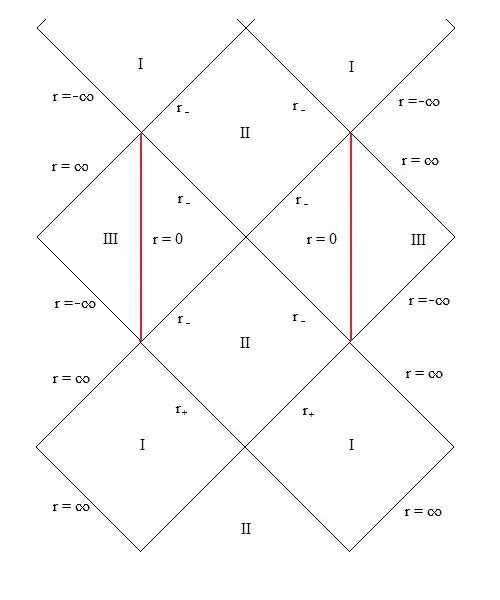
I now turn to the Kerr black hole. This has a ring singularity in the interior. The conformal diagram is seen below

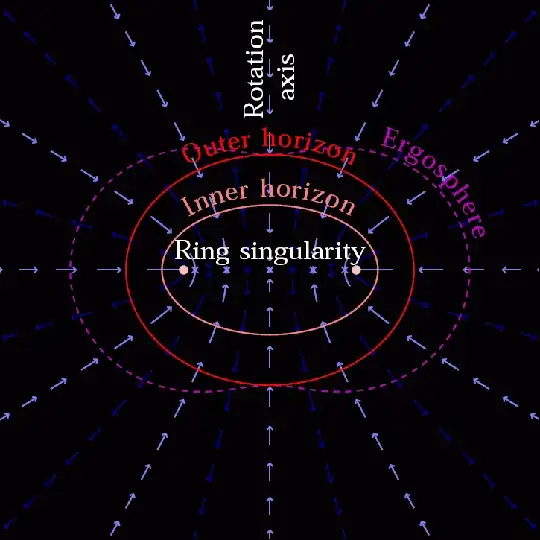
The singularity, which is a ring, is timelike and represented by a vertical line. In this case there is no spatial content, the singularity is a one dimensional object that is also a closed timelike curve. If one thinks a moment it is evident that in this case the $3$ to $1$ duality, or a Poincare-like duality between $4$ $1$-forms and $3$-forms is at play here. The Kerr metric adds angular momentum to the black hole, but the same holds for the Kerr-Newman black hole with electric charge. In fact a general BPS charge will do much the same; the singularity of the black hole is not a $3$-surface, but rather a $1$-dimensional line. It is also a closed timelike curve, which as we know violates the Hawking-Penrose energy condition. The contribution of gravity to the energy-momentum of the field, which is negative, in the black hole interior past the inner horizon "twists up spacetime" so it permits closed timelike curves. I have a diagram below I lifted from the NIST website of visualizing black holes for the Kerr metric.

The conformal diagram above shows that the inner horizon as $r_-~=~m~-~\sqrt{m^2~-~a^2}$, for $a~=~J/mc$ or angular momentum per mass, is coincident with ${\cal I}^+$ or $r~=~\infty$. This would mean that an observer who crosses $r_-$ to enter the timelike region with the singularity would encounter a dense pulse of null rays from all radiation that entered the black hole. This piling up of these null rays makes $r_-$ as Cauchy horizon, and this pulse could be nasty. This might mean that $r_-$ is really deformed into a singularity similar to the Schwarzschild metric singularity. On the other hand due to Hawking radiation $r_-$ and ${\cal I}^+$ are not necessarily coincident, which would soften the "blow." In addition the infalling observer may also be moving on a frame where this pulse of radiation is redshifted enough.

Are these two related further? Does this duality between $1$ and $3$ dimensions tell us more about the nature of black holes and fields? Maybe. The Kerr metric and related metrics for charges on black holes, which for tiny black holes can include QCD color etc, defines a set of hair on the horizon. This hair is entangled with the fields in the far interior of the black hole. I refer to Susskind et al on ER=EPR on this. The Schwarzschild black hole just involves mass, and its singularity is on a spatial surface. The content of the Schwarzschild black hole interior is then due to a field that is entirely gravitational and where the horizon is stitched together by the entanglement structure of fields. The Kerr and related black holes have additional content, say extremal or BPS charges. I might then offer the conjecture that the $1$ dimensional singularity and the $3$ dimensional singularity reflect a duality between the coset entanglement groups of black holes and the structure of field theories other than gravity.