Ring singularity of Kerr metric

Question

I have been reading about the Kerr metric using various sources (Wald's textbook, Visser's The Kerr spacetime: A brief introduction etc.). I could not understand exactly why the singularity structure of the Kerr metric is supposed to be in the form of a ring. Is there an "algebraic derivation" of this in an appropriately chosen coordinate system?

Answer 1

I will not reproduce the derivation, but Ellis and Hawking sketch this in their book "Large Scale Structure of Space-Time" on page 162. One first transforms from the time-radial-angular coordinates to $x,~y,~z, t$. The metric assumes a certain form so the condition $$ r^4~-~r^2(x^2~+~y^2~+~z^2~-~a^2)~-~a^2z^2~=~0 $$ obtains. Here $a~=~J/mc$. Then for $z~=~0$ this reduces to $$ r^2~-~(x^2~+~y^2~-~a^2)~=~0. $$ This defines a family of ellipsoids.

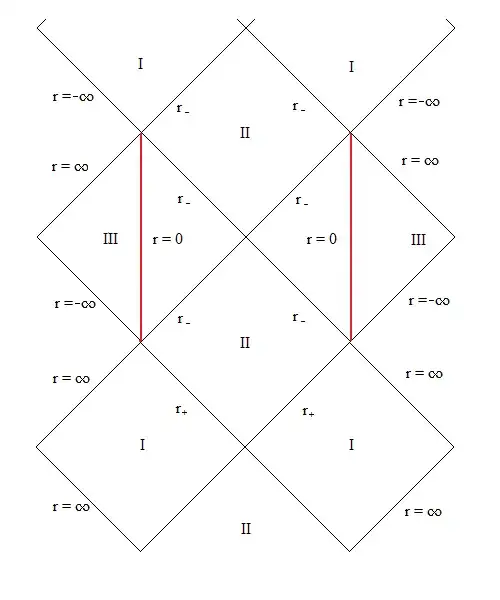
The principal curvature components is $$ R_{rtrt}~=~-\frac{2m}{r^3}, $$ and these hyperboloids give $r~=~\pm\sqrt{x^2~+~y^2~-~a^2}$ and this singularity is seen to be the ring $x^2~+~y^2~=~a^2$. The disk bounded by this ring with $x^2~+~y^2~<~a^2$ is not singular. The two signs for the radius represent to Riemann sheets, where the disk is a form of branch cut. An observer that crosses the disk enters different regions with alternating signs for $r$, in a double covering analytic continuation.

It is not clear whether this singularity actually exists or not. An observer that crosses the inner horizon $r_-$ also crosses the horizon at $\infty$ or ${\cal I}^+$. There will then be a large occurrence of quanta at this region, which might be a Cauchy singularity. So the split $r_-$ might in fact be a type of singularity. The region III with the ring singularity might be a sort of mathematical fiction.