What did general relativity clarify about Mercury?

Question

I frequently hear that Kepler, using his equations of orbital motion, could predict the orbits of all the planets to a high degree of accuracy -- except Mercury. I've heard that mercury's motion couldn't be properly predicted until general relativity came around. But what does general relativity have to do with Mercury's orbit?

Answer 1

This web page has a nice discussion on it: http://archive.ncsa.illinois.edu/Cyberia/NumRel/EinsteinTest.html

Basically the orbit's eccentricity would precess around the sun. Classical stellar mechanics (or Newtonian gravity) couldn't account for all of that. It basically had to do with (and forgive my crude wording) the sun dragging the fabric of space-time around with it.

Or as the web page says:

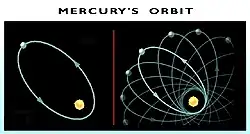
Mercury's Changing Orbit

In a second test, the theory explained slight alterations in Mercury's orbit around the Sun.

Daisy petal effect of precession

Since almost two centuries earlier astronomers had been aware of a small flaw in Mercury's orbit around the Sun, as predicted by Newton's laws. As the closest planet to the Sun, Mercury orbits a region in the solar system where spacetime is disturbed by the Sun's mass. Mercury's elliptical path around the Sun shifts slightly with each orbit such that its closest point to the Sun (or "perihelion") shifts forward with each pass. Newton's theory had predicted an advance only half as large as the one actually observed. Einstein's predictions exactly matched the observation.

For more detail that goes beyond a simple layman answer, you can check this page out and even download an app that let's you play with the phenomenon: http://www.fourmilab.ch/gravitation/orbits/

And of course, the ever handy Wikipedia has this covered as well: http://en.wikipedia.org/wiki/Tests_of_general_relativity#Perihelion_precession_of_Mercury Although, truth be told, I think I said it better (i.e. more elegantly) than the Wiki page does. But then I may be biased.

Answer 2

Mercury's orbit is elliptical. The orientation of this ellipse's long axis slowly rotates around the sun. This process is known as the "precession of the perihelion of Mercury" in astronomical jargon. It's a total of 5600 arcseconds of rotation per century.

The precession is mostly a result of totally classical behavior; almost all of the movement of the perihelion (about 5030 arcseconds per century) is present in a two-body system with point masses for the Sun and Mercury. Another 530 arcseconds per century are caused by gravitational effects of the other planets.

That leaves 40 arcseconds per century of unexplained movement. The observed value of 5599.7 arcseconds per century is measured very accurately, to within 0.04 arcseconds per century, so this is a significant deviation.

It turns out that 43 arcseconds per century are expected to result from general relativity. One hand-wavey way of explaining this is that the curvature of spacetime itself by the two bodies (Sun and Mercury) causes some changes to the gravitational potential, so it isn't really exactly $\frac{GMm}{r}$.

Answer 3

I'd like to add a clarification to the other answers, some of which seem to imply that the precession of Mercury's orbital perehelion is owing to general relativistic frame dragging. In particular, the statement that the Sun drags the fabric of space time around with it could be, in my opinion, misleading because most of the precession is NOT owing to "frame dragging", which is otherwise known as the Lense-Thirring Effect.

A nonrotating Sun would also beget the observed anomalous precession, whose non-Newtonian component almost wholly arises from the inverse cubic term in the effective potential coming from the solution of the Einstein Field Equations for the Schwarzschild Metric. This metric assumes the central body (Sun in this case) is stationary and nonrotating. It is this cubic term that leads to the celebrated triumph of GR over Newtonian gravity, which does not imply this cubic term.

This is the metric that is equivalent Einstein's own analysis used to declare that general relativity explains the anomalous precession. He did not account for the Lense-Thirring frame dragging owing to the Sun's rotation, which is a much smaller effect even than that of the cubic term.

Afternote: Einstein's own method did not solve for a metric; historically, as noted by Physics SE use Stan Liou (thanks Stan):

...[Einstein] used an approximation scheme without writing any metric for his second approximation--but his potential did indeed have an inverse-cube term. Other than via Schwarzschild, a modernized approach would a stationary PPN metric (so no frame dragging here either):

$$\mathrm{d}s^2 = -(1+2\beta\Phi)\mathrm{d}t^2 + (1-2\gamma\Phi)\mathrm{d}\Sigma_\text{Euclid}^2$$

with the perihelion shift scaling proportionally to $(2-\beta+2\gamma)/3$ of the correct GTR value, which predicts $\beta=\gamma=1$

Answer 4

The corrections arising from the Schwarzschild solution, compared to the dynamics given by Newtonian gravity, are small, but apply to all bodies orbiting the sun, not just Mercury. But, Mercury is the flightiest of the planets - which is why it got its name - and the correction happens to be proportional to the square of the "areal velocity" (i.e. angular momentum per unit mass) and inversely proportional to the square of the distance from the sun. It's close to the sun and it's whipping around pretty fast, so it's got the biggest correction.

Without going through the derivation in detail (instead, I derive it here Modified Kepler Equation), the equations for orbital dynamics: $$\frac{d^2}{ds^2} = -\frac{μ}{r^3},\quad \frac{dt}{ds} = 1,\label{0}\tag{Newtonian}$$ where $μ = G M$, with $G$ being Newton's coefficient, $$ the position vector centered on the Schwarzschild object (here: the sun), $r = ||$ is the distance to the object, and $M$ the mass of the object, are corrected to: $$\frac{d^2}{ds^2} = -\frac{μ}{r^3}\left(1 + \frac{3α}{r^2}\left|×\frac{d}{ds}\right|^2\right),\quad \frac{dt}{ds} = \frac{Ar}{r - 2αμ}\label{1}\tag{Einsteinian},$$ where the "time-warping" factor $A$ is determined as the positive solution to the equation $$1 = \frac{r - 2αμ}{r} \left(\frac{dt}{ds}\right)^2 - α \left(\left|\frac{d}{ds}\right|^2 + \frac{2αμ}{r - 2αμ} \left(\frac{dr}{ds}\right)^2\right).$$ This equation and the (\ref{1}) equation hold for "time-like" geodesics; i.e. orbital trajectories for sub-light-speed bodies.

The correction is parametrized by $α = 1/c^2$, where $c$ is light speed. In the limit $c → ∞$, the parameter $α → 0$, and the equation (\ref{1}) → (\ref{0}).

The areal velocity is given by the vector $$ = ×\frac{d}{ds},$$ which is a constant of motion for the equations above and is just $h = ||$. Using it, you can write $$\left|\frac{d}{ds}\right|^2 = \left(\frac{dr}{ds}\right)^2 + \frac{h^2}{r^2},$$ and $$\frac{d^2}{ds^2} = -\frac{μ}{r^3}\left(1 + 3α\frac{h^2}{r^2}\right).$$ The equation for the time-warping factor $A$ reduces to: $$1 = \frac{A^2 r}{r - 2αμ} - α \left(\frac{r}{r - 2αμ}\left(\frac{dr}{ds}\right)^2 + \frac{h^2}{r^2}\right),$$ or, taking the positive root: $$A = \sqrt{\frac{r - 2αμ}{r}\left(1 + α\frac{h^2}{r^2}\right) + α \left(\frac{dr}{ds}\right)^2}.$$

Answer 5

According to Newton's theory (or Kepler's laws of planetary motion), planets are revolving around the sun in closed orbits. But precise astronomical observation found that Mercury's orbit is not closed, but is constantly shifting. The perihelion position of Mercury's orbit has a maximum shifting, about 43 arcs per century. If one calculats the orbits of planets, one immediately sees that if gravitational force follows accurately inverse square law, then the orbits are all closed ellipses. But Einstein found that, his general relativity adds another fourth power term into the equation of gravitational force. This extra term is small compared to its major inverse square term, but enough to account for the perihelion motion of Mercury's pesky orbit.

Answer 6

The solution of Einstein, contesting Newton´s laws, was challenged by several scientists including Dr. Thomas Van Flandern astronomer who worked at the U.S. Naval Observatory in Washington. According to them, Einstein would have gotten this information (43 "arc) and" adjusted "the arguments for the result of the equation, previously known, were achieved, because I knew this would be a critical test for his Theory of General Relativity, http:/ / ldolphin.org / vanFlandern /, www.metaresearch.org, "The Greatest Standing Errors in Physics and Mathematics" in http://milesmathis.com/merc.html Is better believe in the Newton´s laws. The mass that caused the precession of Mercury is shown briefly in 2014.