Understanding thermal radiation in a conductor, gas and insulator

Question

Context:

I was in my bliss of ignorance and happiness when I was taught that quantum mechanics was about nice discrete values of energies. Now I am introduced the idea of Fermi Energy in a block of solid and I have to face the fact that we are getting continuous spectrum out of everything, from the sun to a light bulb to a rock. Quantum is not quantum anymore.

Question:

1. Right or Wrong: Thermal radiation's spectrum is continuous for earthly normal objects like a lite light bulb or a conductor, it is because once you plug every electron in the solid into a giant quantum mechanics equation, I personally call it a "giant fermi pool" while obeying the Pauli exclusion principle, I will end up with many energy levels for trillions of electrons, those levels are going to be quite continuous.

2. Right or Wrong: Gas under atm pressure doesn't emit continuous spectrum, because their atom's electrons are so far apart, they are not interacting, each atom's electrons are in their own isolated "fermi pool". Different atoms can have electrons of the same energy state.

3. Right or Wrong: A block of insulator will have a discontinuous thermal radiation spectrum at some temperature as its "internal conditions" (like crystal lattice or boundary condition) just won't allow some energy state to exist.

Answer 1

Terms black-body radiation and thermal radiation are not really interchangeable. It becomes even more ambiguous when we discuss which type of radiation is emitted by thermal light sources. Judging by some discussions in this community (e.g., Black body vs. Thermal radiation) the definitions are not generally agree upon, so what follows is intended to help to sort things our, rather than as the ground truth.

Black-body radiation is an equilibrium state of a photon gas (i.e., of the electromagnetic field). As long as we are talking about free space, this photon gas has continuous spectrum, and the spectrum is given by the Planck formula. If we discussed the EM field inside a resonator, it would likely have discrete spectrum, and its thermal state would be characterized by a discrete spectrum as well. (However, if the resonator has black walls, the spectrum would be still continuous.)

Thermal radiation is radiation emitted by thermal light sources, which I define as objects at certain temperature (i.e., objects that can be considered internally in thermal equilibrium, but not necessarily in equilibrium with the surrounding EM field). The properties of these objects determine the frequencies of the radiation that they emit and thus its spectrum. In the spirit of the OP I mentione a few cases:

• An electron gas, in which electrons collide with each other, emitting on all possible frequencies (Thermal Bremsstrahlung). The radiation emitted by such a gas will be from the beginning very close to the black body spectrum.
• Gas of atoms. Atoms emit at discrete frequencies, but these will be broadened due to the Doppler effects. Further, higher order processes, such as Raman scattering, can couple this discrete spectrum to the continuoum of electromagnetic modes. Thus, the radiation initially emitted at discrete frequencies will eventually evolve towards the black body spectrum.
• Semiconductor/insulator has a well-defined cutoff frequency: very little is emitted below the gap (mainly discrete frequenices due to the impurity levels and excitons), but the spectrum above the gap is continuous. This will also eventually evolve towards the black body spectrum due to the higher order processes.

How thermal radiation becomes black body radiation
I have already mentioned above that the higher order processes typically pump the energy ito the modes weakly coupled to the thermal light source. It may take very long time in some cases - even infinitely long time (in which case we might talk about phase transitions - like the polarization of a ferromagnet that remains stuck in one energy minimum, despite the availability of the other states of the same energy.) Equilibrium statistical phsyics however deals with equilibrium states, without caring for how they are established. And many examples of thermal radiation can be safely assume to have black body spectrum (as if these bodies were coupled to all electromagnetic modes withe qual strength - the definition of a black body.) See thsi thread for examples: How does radiation become black-body radiation?

Answer 2

Right or Wrong: Thermal radiation's spectrum is continuous for earthly normal objects like a lite light bulb or a conductor, it is because once you plug every electron in the solid into a giant quantum mechanics equation, I personally call it a "giant fermi pool" while obeying the Pauli exclusion principle, I will end up with many energy levels for trillions of electrons, those levels are going to be quite continuous.

Wrong. Thermal radiation is all about photons. It is obtained, when the modes of electro-magnetic cavity (e.g. vacuum inside a box) are occupied according to Bosonic statistics. The box can be imagined infinite, and one get's continuum of photon states, and the number of photons in each state is given by the Bose-Einstein distribution. In other words, the electrons and nuclei of the 'metal' of the black box plays only a very minor role here. There is some particular light-matter interaction between the matter and the photons in the box. The exact form of this interaction does not matter to the end result. It is just sufficient that there is some interaction. Now, if the electrons and nuclei of the metal have a different temperature, mediated through light-matter interaction, heat will flow to the photon modes of the cavity until the light and the matter are in thermal equlibrium. This is related to the equipartition theorem, which needs to be applied to quantum energy levels of photons in order to avoid the ultraviolet catastrophe.

Right or Wrong: Gas under atm pressure doesn't emit continuous spectrum, because their atom's electrons are so far apart, they are not interacting, each atom's electrons are in their own isolated "fermi pool". Different atoms can have electrons of the same energy state.

Wrong. As discussed in part 1. the continuous spectrum is all about the photons being in thermal equilibrium. Thermal emission on atoms occurs when the temperature is sufficient large so that an electron can be thermally excited. This excited state of an atom does then couple only to very special modes of the cavity, namely to those which preserve energy and momentum. Therefore, one obtains sharp peak of photon energies when observing emission.

Right or Wrong: A block of insulator will have a discontinuous thermal radiation spectrum at some temperature as its "internal conditions" (like crystal lattice or boundary condition) just won't allow some energy state to exist.

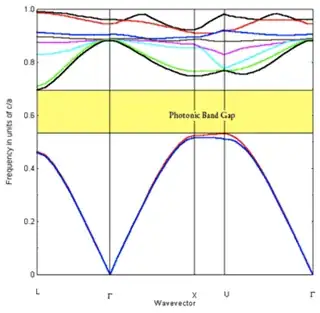
Wrong again, I'm afraid. It is true that semiconductors and insulators have forbidden single-particle levels, for example so that there is a gap between their photoemission and inverse-photoemission spectra. But the idea is correct, since there actually exists structures which have a photonic-band gap. Similarly to the electrons, given certain geometry of the cavity, photons too can have band gaps. Due to geometry (for example a periodic lattice of metal beads in a transparent substrate) there are forbidden energy-levels for photons. Keywords: opals (yes, the common gems have a band gap in such that particular wave lengths of light cannot propagate in them), photonic crystals.

Here is an example band structure for photons, which shows the photonic band gap