I will try to answer as many questions as I can. I won't presume to give you complete exhaustive answers, but maybe they will be nonetheless useful to you.
What variables determine the range of temperatures over which matter is liquid? My understanding of thermodynamics is that matter changes from a solid to a gas when some thermal vibrations create an effective repulsion of sufficient magnitude to overcome the forces of attraction between particles. But a balance of these two forces only gives rise to two phases - the "attraction < repulsion" phase, and the "attraction > repulsion" phase. A second inequality seems necessary to get three phases; what is it? I guess pressure must be involved, but how?
I think that it is better to reason in the following way: if $K$ is the total kinetic energy and $U$ is the absolute value of the total potential energy, you will have
- $K/U \ll 1$ for the solid
- $K/U \gg 1$ for the gas
- $K/U \simeq 1$ for the liquid
Do classical "billiard ball" computer simulations give rise to solid-liquid-gas phenomena? I'm talking about simulations with identical hard spheres bouncing off of each other without friction. If not, what is the smallest modification to such simulations which is necessary to observe liquids? For instance, is it sufficient to modify the potential barrier between particles to be somewhat smooth (rather than an infinite step function as for hard spheres)?
System of hard spheres have been extensively studied theoretically and with simulations and nowadays we know quite a lot about them. In the following picture, you can see the phase diagram of an hard-sphere system:
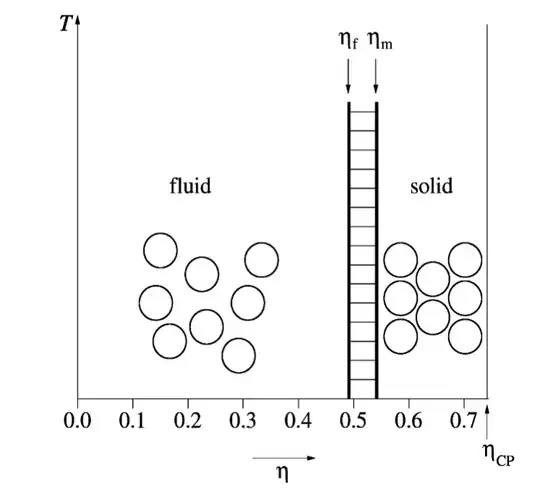
The first thing you will notice is that temperature is irrelevant for the phase behavior of such a system. This is because the only interaction is the "infinite step function" you mentioned, so changing the temperature will just make the dynamics of the system faster or slower but won't change the average intensity of the interaction (because the potential energy is simply $0$).
The phase behavior is only controlled by the packing fraction
$$\eta = \frac \pi 6 \rho \sigma^3$$
Where $\rho$ is density and $\sigma$ is the diameter of a sphere. The packing fraction is just the fraction of the total volume which is occupied by the spheres.
You can see that the system has only two phases: fluid and solid. The fluid freezes at $\eta_f=0.494$ and the solid melts at $\eta_m=0.545$. Between those two values fluid and solid are at equilibrium. The maximum value of $\eta$ is the close-packing packing fraction $\eta_{CP}=\pi \sqrt{2}/6\simeq0.74$ and it is realized for cristalline hcp or fcc arrangements.
So there is only one "fluid" state for hard spheres: there are no "gas" and "liquid" phases. So there is no liquid phase in an hard sphere system. To have a liquid state, it turns out, we must introduce some sort of attraction: even a square well potential is sufficient.
To quote Hansen-McDonald (Theory of Simple Liquids):
The most important feature of the pair potential between atoms or molecules is the harsh repulsion that appears at short range and has its origin in the overlap of the outer electron shells. The effect of these strongly repulsive forces is to create the short-range order that is characteristic of the liquid state. The attractive forces, which act at long range, vary much more smoothly with the distance between particles and play only a minor role in deter- mining the structure of the liquid. They provide, instead, an essentially uniform, attractive background and give rise to the cohesive energy that is required to stabilise the liquid.
So to have a liquid you need repulsion (and that's in a certain way the most important thing), but also attraction. It is not sufficient to modify the repulsive barrier to make it smooth: you have to make it (partly) attractive!
Alternatively, is quantum mechanics necessary for a correct description of the phenomenon of liquidity? Is it necessary to invoke superconductivity (e.g. of phonons)?
No, superconductivity and phonons are not really necessary. And quantum mechanics isn't either. I mean, if you want to find the exact function describing the inter-molecular forces in a liquid you will need to take QM into account. But simple models are more than sufficient to understand the physics of liquids. You could take a square well,a Yukawa or a Lennard-Jones potential and the system will always show a liquid phase with a qualitatively similar behavior. In general, QM becomes important when the De Broglie thermal wavelength of the particles
$$\lambda = \sqrt{\frac{2 \pi \beta \hbar^2}{m}}$$
is of the order of the mean nearest-neighbour separation,
$$a\simeq \rho^{-1/3}$$
For most liquids (an exception being for example $^4$He which becomes a superfluid in a certain pressure-density region), quantum mechanical effects can be completely neglected.
Anyway, to conclude, I would suggest that you tried to think about the free energy $F=U-TS$. A system will always try to minimize its free energy. At low temperatures, the $TS$ term won't be so important so the system will minimize $U$ forming as many bonds as it can (the solid state). At high temperatures the $TS$ term will be more important so it will try to attain the most disordered, high entropy state it can attain (the gaseous state). But at intermediate temperatures, when both terms are important, it will find a "balance" between energy and entropy, and from this balance the liquid state will result.
Remember: the liquid state is no easy business to study!
The classical fluid is perhaps not everyone's cup of tea
-N. W. Ashcroft